Lim 1/n

Show that Lim 1/n = 0

|1/n-0|< ε => |1/n| < ε so n > 1/ε.

Now do I say take δ > 1/ε?

n increases to infinity. So you need 'take N > 1/e. For all n >= N...'
something like that.

Given e > 0, take N > 1/e, then |x-a| < N => |1/n| < e => |f(x)-L| < e.

Is that correct?

Show that Lim 1/n = 0

|1/n-0|< ε => |1/n| < ε so n > 1/ε.

Now do I say take δ > 1/ε?

Make sure you understand the difference between the definition for the limit of a function at a point where you use e-d and the definition for a sequence at infinity where you use N. good luck

Thanks, I didn't realise that there was a distinction. Could you explain this, please.

With a sequence tending to infinity say you wish to find a value such that given any number you can find another number such that for all values in the sequence bigger than the second number the sequence is bigger than the first number.

So an example, suppose our sequence is given by a_n=n for all natural numbers.

Then this sequence you will recognise as this 1,2,3,4,5,6,..... and so on. Now you can give me any number greater that 0 so 500 for example and I can give you another number 1000 for example such that every term in the sequence bigger than the 1000th term the value of the sequence is bigger than 500. (Of course 500 would also work so would 777 or 20000 for that matter as all terms after any of these are certainly bigger than 500.)

That is showing a sequence tends to infinity.

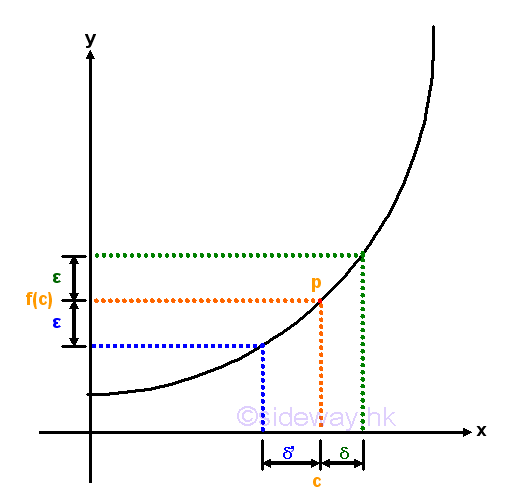
To show a function converges to a real number l. Then you need to show you can get as close to l as you want as long as we get close to some number .

Example let the sequence be f(x)=x for all natural numbers n then I can give you any positive number (epsilon is used and is normally small as well because we want the distance from the limit to be small normally as well.) Now it's clear that x goes to 0 as n goes to 0 but how close does x have to be to zero so that the function is close enough to zero. Well this is where delta comes in. We aim to show that given any epsilon greater than zero (1 or 0.1 or 0.000000005 etc)
we can get within epsilon either side of zero. You have to do some algebraic manipulation in order to find a delta that will make you close enough to be within epsilon of the limit.

I don't think I've explained this great but hopefully it helps a little. There are some way better resources out there so take a look at them and also look at some of the visual stuff because that really helps the concepts become easier to understand in my opinion.