The Student Room Group
Uni students - Complete our survey >>
Uni students - Complete our survey >>
Uni students - Complete our survey >>

The Proof is Trivial!

Scroll to see replies

Original post by Star-girl
Solution 56

By the t-substitution t=tan⁡12xt=\tan \dfrac{1}{2} x , the limits get transformed into t2=tan⁡12⋅2π=0, t1=tan⁡12⋅0=0t_2= \tan \dfrac{1}{2} \cdot 2\pi = 0 ,\ t_1 = \tan \dfrac{1}{2} \cdot 0 = 0 and since the limits are the same, the integral evaluates to 0 0 .

I get π6\dfrac{\pi}{\sqrt{6}} :s-smilie:
Original post by Felix Felicis
I get π6\dfrac{\pi}{\sqrt{6}} :s-smilie:


Seems more plausible than 0. My solution is probably dodgy then... but why? :holmes:
Reply 422
Avatar for und
und
OP
16
Original post by Star-girl
Solution 56

By the t-substitution t=tan⁡12xt=\tan \dfrac{1}{2} x , the limits get transformed into t2=tan⁡12⋅2π=0, t1=tan⁡12⋅0=0t_2= \tan \dfrac{1}{2} \cdot 2\pi = 0 ,\ t_1 = \tan \dfrac{1}{2} \cdot 0 = 0 and since the limits are the same, the integral evaluates to 0 0 .

Seems a bit too quick - maybe this is a little dodgy...

The integrand is positive over the interval, so it's impossible for the integral to be 0.
Original post by Star-girl
Seems more plausible than 0. My solution is probably dodgy then... but why? :holmes:

Maybe because of the asymptotes of tan between the limits? :holmes:
Original post by und
The integrand is positive over the interval, so it's impossible for the integral to be 0.


Original post by Felix Felicis
Maybe because of the asymptotes of tan between the limits? :holmes:


Ha! What a noobish error I made... I think it's sleepy-time for me... :facepalm:
(edited 11 years ago)
Solution 56

56 Solution

(edited 10 years ago)
Reply 426
Avatar for und
und
OP
16
Original post by MsDanderson
hey! IF YOU'RE A FEMALE, could you fill this out please? it literally only takes 2mins do it -> http://www.surveymonkey.com/s/B3MVL58

I need 100 done in the next 24 hours or I'll fail my project :frown: Please help! I'm so grateful

You come looking for females... in a maths thread?
Original post by und
You come looking for females... in a maths thread?

I only just read that it's for females...I already filled it in :facepalm: Ah well :colone:
Original post by MsDanderson
it's okay! i appreciate it anyway!

You might want to discard my results anyway...my answers may skew your data for a survey targeted at females to put it lightly :colone:
Reply 429
Avatar for james22
james22
16
Original post by Star-girl
Solution 56

By the t-substitution t=tan⁡12xt=\tan \dfrac{1}{2} x , the limits get transformed into t2=tan⁡12⋅2π=0, t1=tan⁡12⋅0=0t_2= \tan \dfrac{1}{2} \cdot 2\pi = 0 ,\ t_1 = \tan \dfrac{1}{2} \cdot 0 = 0 and since the limits are the same, the integral evaluates to 0 0 .

Seems a bit too quick - maybe this is a little dodgy...

EDIT: Ignore this rubbish.


Can't just sub in t=tan(x/2) as it is not continuous across the range of integration.
Reply 430
Avatar for und
und
OP
16
Problem 59**

Prove that there are no integers x,yx,y for which x2+3xy−2y2=122x^2+3xy-2y^2=122.
(edited 11 years ago)
Original post by dknt
Well I guess I'll provide another physicsy mathsy problem :colone:

Problem 58 **/***

A double pendulum consists of a mass m2 suspended by a rod of length l2 from a mass m1, which is itself suspended by a rod of length l1 from a fixed pivot, as shown below.

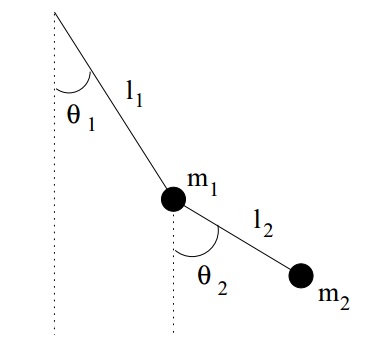
Untitled.jpg

Show that the equations of motion for small displacements can be written as

MΘ¨=−KΘM \ddot{\Theta} = -K \Theta where,

M=(l12(m1+m2)l1l2m2l1l2m2l22m2)M= \begin{pmatrix} {l_1} ^2(m_1 +m_2) & l_1 l_2 m_2 \\l_1 l_2 m_2 & {l_2} ^2 m_2 \end{pmatrix}

K=(gl1(m1+m2)00gl2m2) K = \begin{pmatrix} gl_1 (m_1 +m_2) & 0 \\ 0 & gl_2 m_2 \end{pmatrix}

and Θ=(θ1θ2) \Theta = \begin{pmatrix} \theta_1 \\ \theta_2 \end{pmatrix}


Spoiler

Reply 432
Avatar for dknt
dknt
12
Original post by cpdavis

Spoiler



Spoiler

(edited 11 years ago)
Original post by dknt

Spoiler



Spoiler

Original post by bananarama2
I just lost the will to live with that question after I completed a load of school work (binomial expansion). I generally go for energy, but just didn't in that instance, nice one Star-girl (I had to think about that name.)


For some reason I didn't see this yesterday. Ah yes... school work... what I should have been doing this holiday... :ninjagirl:

Thanks (and haha). :cute:
Original post by und
You come looking for females... in a maths thread?


:colone:

Original post by james22
Can't just sub in t=tan(x/2) as it is not continuous across the range of integration.


Yeah - I realised afterwards, hence the edits...
(edited 11 years ago)
Reply 436
Avatar for Mladenov
Mladenov
1
Solution 59

More general:

Denote f(x,y)=ax2+bxy+cy2f(x,y)=ax^{2}+bxy+cy^{2}. This is called binary quadratic form. Its discriminant is defined as Δ=b2−4ac \Delta= b^2-4ac.
We say that ff represents given number nn properly if there are integers x0,y0x_{0},y_{0} such that f(x0,y0)=nf(x_{0},y_{0})=n and gcd⁡(x0,y0)=1\gcd(x_{0},y_{0})=1.

We have the following proposition:
Let n≠0n \not= 0 and dd be given integers. Then there exists a binary quadratic form of discriminant dd that represents nn properly if and only if x2≡d(mod4∣n∣)x^2 \equiv d \pmod {4|n|} is solvable.

Let gcd⁡(x0,y0)\gcd(x_{0},y_{0}) and f(x0,y0)=nf(x_{0},y_{0})=n. Since gcd⁡(x0,y0)=1\gcd(x_{0},y_{0})=1, we can choose integers n1,n2n_{1},n_{2} such that n1n2=4∣n∣n_{1}n_{2}=4|n|, gcd⁡(n1,n2)=1\gcd(n_{1},n_{2})=1, gcd⁡(n1,x0)=1\gcd(n_{1},x_{0})=1, and gcd⁡(n2,y0)=1\gcd(n_{2},y_{0})=1. Notice that 4an=(2ax0+by0)2−dy024an=(2ax_{0}+by_{0})^{2}-dy_{0}^{2}. Now there are integers k1,k2k_{1},k_{2} such that k12≡d(modn1)k_{1}^{2} \equiv d \pmod {n_{1}} and k22≡d(modn2)k_{2}^{2} \equiv d \pmod {n_{2}}. It remains to cite the Chinese remainder theorem.
Conversely, let b2−d=4cnb^2-d=4cn. Then the form f(x,y)=nx2+bxy+cy2f(x,y)=nx^{2}+bxy+cy^{2} has discriminant dd and represents nn properly.

Next, I claim that there is not binary quadratic form of discriminant d=17d=17 which represents 122122 properly. Since 122122 is square-free, we cannot have improper representations.
The congruence x2≡17(mod8)x^{2} \equiv 17 \pmod8 is obviously solvable. Consider the congruence x2≡17(mod61)x^{2} \equiv 17 \pmod {61}. Now (1761)(1017)=(1761)(217)(517)=(1761)(25)=−(1761)=1\left(\frac{17}{61} \right)\left(\frac{10}{17} \right)=\left(\frac{17}{61} \right)\left(\frac{2}{17} \right)\left(\frac{5}{17} \right)=\left(\frac{17}{61} \right)\left(\frac{2}{5} \right)=-\left(\frac{17}{61} \right)=1. Hence (1761)=−1\left(\frac{17}{61} \right)=-1. Therefore the congruence x2≡17(mod4×122)x^{2} \equiv 17 \pmod {4\times 122} has no solutions and my claim holds true.
Solution 58

x1=l1sin⁡θ1 x_1 = l_1 \sin \theta_1

x1˙=l1θ1˙cos⁡θ1 \dot{ x_1 } = l_1 \dot{ \theta_1} \cos \theta_1

y1=l1cos⁡θ1 y_1 = l_1 \cos \theta_1

y1˙=−l1dotθ1sin⁡θ1 \dot{ y_1} = -l_1 dot{ \theta_1} \sin \theta_1

x2=l1sin⁡θ1+l2sin⁡θ2 x_2 = l_1 \sin \theta_1 + l_2 \sin \theta_2

x2˙=l1θ1˙cos⁡θ1+l2θ2˙cos⁡θ2 \dot {x_2} = l_1 \dot{ \theta_1 } \cos \theta_1 + l_2 \dot{ \theta_2} \cos \theta_2

y2=l1cos⁡θ1+l2cos⁡θ2 y_2 = l_1 \cos \theta_1 + l_2 \cos \theta_2

y2˙=−l1θ1˙sin⁡θ1−l2θ2˙sin⁡θ2 \dot {y_2} = -l_1 \dot{ \theta_1 } \sin \theta_1 - l_2 \dot{ \theta_2} \sin \theta_2


L=12m1l12θ1˙2+12m2(l1θ1˙cos⁡θ1+l2θ2˙cos⁡θ2)2+12m2(−l1θ1˙sin⁡θ1−l2θ2˙sin⁡θ2)2+m1gl1cos⁡θ1+m2g(l1cos⁡θ1+l2cos⁡θ2)\displaystyle \mathcal{ L} = \frac{1}{2} m_1 l_1^2 \dot{ \theta_1}^2 + \frac{1}{2} m_2 \left( l_1 \dot{ \theta_1 } \cos \theta_1 + l_2 \dot{ \theta_2} \cos \theta_2 \right)^2 + \frac{1}{2}m_2 \left(-l_1 \dot{ \theta_1 } \sin \theta_1 - l_2 \dot{ \theta_2} \sin \theta_2 \right)^2 + m_1 g l_1 \cos \theta_1 + m_2 g ( l_1 \cos \theta_1 + l_2 \cos \theta_2 )

=12m1l12θ1˙2+12m2l12θ1˙2+12m2l22θ2˙2+m2l1l2cos⁡(θ1−θ2)θ1˙θ2˙+m1gl1cos⁡θ1+m2g(l1cos⁡θ1+l2cos⁡θ2)\displaystyle = \frac{1}{2} m_1 l_1^2 \dot{ \theta_1}^2 + \frac{1}{2}m_2 l_1^2 \dot{\theta_1}^2 + \frac{1}{2}m_2l_2^2 \dot{\theta_2}^2 + m_2 l_1 l_2 \cos (\theta_1 - \theta_2 ) \dot{ \theta_1} \dot{ \theta_2} + m_1 g l_1 \cos \theta_1 + m_2 g ( l_1 \cos \theta_1 + l_2 \cos \theta_2 )

∂L∂θ1=−m2l1l2sin⁡(θ1−θ2)θ1˙θ2˙−m1gl1sin⁡θ1−m2gl1sin⁡θ1\displaystyle \frac{\partial \mathcal{ L}}{\partial \theta_1}= -m_2 l_1 l_2 \sin ( \theta_1 - \theta_2 ) \dot{ \theta_1} \dot{ \theta_2} - m_1 g l_1 \sin \theta_1 -m_2 g l_1 \sin \theta_1

≈−m2l1l2(θ1−θ2)θ1˙θ2˙−m1gl1θ1−m2gl1θ1\displaystyle \approx -m_2 l_1 l_2 ( \theta_1 - \theta_2 ) \dot{ \theta_1} \dot{ \theta_2} - m_1 g l_1 \theta_1 -m_2 g l_1 \theta_1

∂L∂θ1˙=m1l22θ1˙+m2l12θ1˙+m2l1l2cos⁡(θ1−θ2)θ2˙ \displaystyle \frac{\partial \mathcal{ L}}{\partial \dot{\theta_1}} =m_1 l_2^2 \dot{ \theta_1} + m_2 l_1^2 \dot{ \theta_1} + m_2 l_1 l_2 \cos ( \theta_1 - \theta_2 ) \dot{ \theta_2 }

ddt(∂L∂θ1˙)=m1l22θ1¨+m2l12θ1¨−(θ1˙−θ2˙)m2sin⁡(θ1−θ2)θ2˙+m2l1l2cos⁡(θ1−θ2)θ2¨\displaystyle \frac{d}{dt} \left( \frac{\partial \mathcal{ L}}{\partial \dot{\theta_1}}\right) = m_1 l_2^2 \ddot{ \theta_1} + m_2 l_1^2 \ddot{ \theta_1} - (\dot{\theta_1}- \dot{\theta_2} ) m_2 \sin (\theta_1-\theta_2 ) \dot{\theta_2} + m_2 l_1 l_2 \cos ( \theta_1 - \theta_2 ) \ddot{ \theta_2}

≈m1l22θ1¨+m2l12θ1¨−(θ1˙−θ2˙)m2(θ1−θ2)θ2˙+m2l1l2θ2¨\displaystyle \approx m_1 l_2^2 \ddot{ \theta_1} + m_2 l_1^2 \ddot{ \theta_1} - (\dot{\theta_1}- \dot{\theta_2} ) m_2 (\theta_1-\theta_2 ) \dot{\theta_2} + m_2 l_1 l_2 \ddot{ \theta_2}

ddt(∂L∂θ1˙)−∂L∂θ1=0\displaystyle \frac{d}{dt} \left( \frac{\partial \mathcal{ L}}{\partial \dot{\theta_1}}\right) - \frac{\partial \mathcal{ L}}{\partial \theta_1} = 0

m1l22θ1¨+m2l12θ1¨−(θ1˙−θ2˙)m2(θ1−θ2)θ2˙+m2l1l2θ2¨+m2l1l2(θ1−θ2)θ1˙θ2˙+m1gl1θ1+m2gl1θ1=0\displaystyle m_1 l_2^2 \ddot{ \theta_1} + m_2 l_1^2 \ddot{ \theta_1} - (\dot{\theta_1}- \dot{\theta_2} ) m_2 (\theta_1-\theta_2 )\dot{\theta_2} + m_2 l_1 l_2 \ddot{ \theta_2} +m_2 l_1 l_2 ( \theta_1 - \theta_2 ) \dot{ \theta_1} \dot{ \theta_2} + m_1 g l_1 \theta_1 +m_2 g l_1 \theta_1 =0

m1l22θ1¨+m2l12θ1¨−(θ1˙θ2˙−θ2˙2)m2(θ1−θ2)+m2l1l2θ2¨+m2l1l2θ1θ1˙θ2˙−m2l1l2θ2θ1˙θ2˙+m1gl1θ1+m2gl1θ1=0\displaystyle m_1 l_2^2 \ddot{ \theta_1} + m_2 l_1^2 \ddot{ \theta_1} - (\dot{\theta_1}\dot{\theta_2}- \dot{\theta_2}^2 ) m_2 (\theta_1-\theta_2 ) + m_2 l_1 l_2 \ddot{ \theta_2} +m_2 l_1 l_2 \theta_1 \dot{ \theta_1} \dot{ \theta_2} - m_2 l_1 l_2 \theta_2 \dot{ \theta_1} \dot{ \theta_2} + m_1 g l_1 \theta_1 +m_2 g l_1 \theta_1 =0

m1l22θ1¨+m2l12θ1¨−θ1θ1˙θ2˙m2l1l2+θ1˙θ2˙θ2m2l1l2+θ2˙2θ1m1l1l2−θ2˙2θ2m2l1l2+m2l1l2θ2¨+m2l1l2θ1θ1˙θ2˙−m2l1l2θ2θ1˙θ2˙+m1gl1θ1+m2gl1θ1=0\displaystyle m_1 l_2^2 \ddot{ \theta_1} + m_2 l_1^2 \ddot{ \theta_1} - \theta_1 \dot{\theta_1 } \dot{\theta_2} m_2 l_1 l_2 + \dot{\theta_1} \dot{\theta_2}\theta_2 m_2 l_1 l_2 + \dot{\theta_2}^2 \theta_1 m_1 l_1 l_2 - \dot{\theta_2}^2 \theta_2 m_2 l_1 l_2 + m_2 l_1 l_2 \ddot{ \theta_2} +m_2 l_1 l_2 \theta_1 \dot{ \theta_1} \dot{ \theta_2} - m_2 l_1 l_2 \theta_2 \dot{ \theta_1} \dot{ \theta_2} + m_1 g l_1 \theta_1 +m_2 g l_1 \theta_1 =0

m1l22θ1¨+m2l12θ1¨+θ2˙2θ1m1l1l2−θ2˙2θ2m2l1l2+m2l1l2θ2¨+m1gl1θ1+m2gl1θ1=0\displaystyle m_1 l_2^2 \ddot{ \theta_1} + m_2 l_1^2 \ddot{ \theta_1} + \dot{\theta_2}^2 \theta_1 m_1 l_1 l_2 - \dot{\theta_2}^2 \theta_2 m_2 l_1 l_2 + m_2 l_1 l_2 \ddot{ \theta_2} + m_1 g l_1 \theta_1 +m_2 g l_1 \theta_1 =0

Ignoring none linear terms.

m1l22θ1¨+m2l12θ1¨+m2l1l2θ2¨+m1gl1θ1+m2gl1θ1=0\displaystyle m_1 l_2^2 \ddot{ \theta_1} + m_2 l_1^2 \ddot{ \theta_1} + m_2 l_1 l_2 \ddot{ \theta_2} + m_1 g l_1 \theta_1 +m_2 g l_1 \theta_1 =0

∂L∂θ2=m2l1l2sin⁡(θ1−θ2)θ1˙θ2˙−m2gl2sin⁡θ2 \displaystyle \frac{\partial \mathcal{ L}}{\partial \theta_2} = m_2 l_1 l_2 \sin ( \theta_1 - \theta_2 ) \dot{\theta_1} \dot{ \theta_2} - m_2 g l_2 \sin \theta_2

≈m2l1l2(θ1−θ2)θ1˙θ2˙−m2gl2θ2 \displaystyle \approx m_2 l_1 l_2 ( \theta_1 - \theta_2 ) \dot{\theta_1} \dot{ \theta_2} - m_2 g l_2 \theta_2

∂L∂θ2˙=m2l22θ2˙+m2l1l2cos⁡(θ1−θ2)θ1˙\displaystyle \frac{\partial \mathcal{ L}}{\partial \dot{\theta_2}}= m_2 l_2^2 \dot{\theta_2 } + m_2 l_1 l_2 \cos ( \theta_1 - \theta_2 ) \dot{ \theta_1}

ddt(∂L∂θ1˙)=m2l22θ2¨−(θ1˙−θ2˙)m2l1l2sin⁡(θ1−θ2)θ1˙+m2l1l2cos⁡(θ1−θ2)θ1¨\displaystyle \frac{d}{dt} \left( \frac{\partial \mathcal{ L}}{\partial \dot{\theta_1}}\right) = m_2 l_2^2 \ddot{\theta_2} - (\dot{\theta_1} - \dot{\theta_2} )m_2 l_1 l_2 \sin ( \theta_1 - \theta_2 ) \dot{ \theta_1} + m_2 l_1 l_2 \cos (\theta_1 - \theta_2 ) \ddot{ \theta_1}

≈m2l22θ2¨−(θ1˙−θ2˙)m2l1l2(θ1−θ2)θ1˙+m2l1l2θ1¨\displaystyle \approx m_2 l_2^2 \ddot{\theta_2} - (\dot{\theta_1} - \dot{\theta_2} )m_2 l_1 l_2 ( \theta_1 - \theta_2 ) \dot{ \theta_1} + m_2 l_1 l_2 \ddot{ \theta_1}

ddt(∂L∂θ2˙)−∂L∂θ2=0\displaystyle \frac{d}{dt} \left( \frac{\partial \mathcal{ L}}{\partial \dot{\theta_2}}\right) - \frac{\partial \mathcal{ L}}{\partial \theta_2} = 0

m2l22θ2¨−(θ1˙−θ2˙)m2l1l2(θ1−θ2)θ1˙+m2l1l2θ1¨−m2l1l2(θ1−θ2)θ1˙θ2˙+m2gl2θ2=0 \displaystyle m_2 l_2^2 \ddot{\theta_2} - (\dot{\theta_1} - \dot{\theta_2} )m_2 l_1 l_2 ( \theta_1 - \theta_2 ) \dot{ \theta_1} + m_2 l_1 l_2 \ddot{ \theta_1} -m_2 l_1 l_2 ( \theta_1 - \theta_2 ) \dot{\theta_1} \dot{ \theta_2} + m_2 g l_2 \theta_2 =0

Ignoring non linear terms.

m2l22θ2¨+m2l1l2theta1¨=−m2gl2θ2 m_2l_2^2 \ddot{\theta_2} + m_2 l_1 l_2 \ddot{theta_1} = -m_2gl_2 \theta_2

We have

l12(m1+m2)θ1¨+l1l2m2θ2¨=gl1(m1+m2)θ1\displaystyle {l_1} ^2(m_1 +m_2) \ddot{\theta_1} + l_1 l_2 m_2 \ddot{\theta_2} = gl_1 (m_1 +m_2 ) \theta_1

and

m2l22θ2¨+m2l1l2theta1¨=−m2gl2θ2 m_2l_2^2 \ddot{\theta_2} + m_2 l_1 l_2 \ddot{theta_1} = -m_2gl_2 \theta_2

So;

MΘ¨=−KΘM \ddot{\Theta} = -K \Theta where,

M=(l12(m1+m2)l1l2m2l1l2m2l22m2)M= \begin{pmatrix} {l_1} ^2(m_1 +m_2) & l_1 l_2 m_2 \\l_1 l_2 m_2 & {l_2} ^2 m_2 \end{pmatrix}

K=(gl1(m1+m2)00gl2m2) K = \begin{pmatrix} gl_1 (m_1 +m_2) & 0 \\ 0 & gl_2 m_2 \end{pmatrix}

and Θ=(θ1θ2) \Theta = \begin{pmatrix} \theta_1 \\ \theta_2 \end{pmatrix}
Original post by bananarama2
Solution 58

x1=l1sin⁡θ1 x_1 = l_1 \sin \theta_1

x1˙=l1θ1˙cos⁡θ1 \dot{ x_1 } = l_1 \dot{ \theta_1} \cos \theta_1

y1=l1cos⁡θ1 y_1 = l_1 \cos \theta_1

y1˙=−l1dotθ1sin⁡θ1 \dot{ y_1} = -l_1 dot{ \theta_1} \sin \theta_1

x2=l1sin⁡θ1+l2sin⁡θ2 x_2 = l_1 \sin \theta_1 + l_2 \sin \theta_2

x2˙=l1θ1˙cos⁡θ1+l2θ2˙cos⁡θ2 \dot {x_2} = l_1 \dot{ \theta_1 } \cos \theta_1 + l_2 \dot{ \theta_2} \cos \theta_2

y2=l1cos⁡θ1+l2cos⁡θ2 y_2 = l_1 \cos \theta_1 + l_2 \cos \theta_2

y2˙=−l1θ1˙sin⁡θ1−l2θ2˙sin⁡θ2 \dot {y_2} = -l_1 \dot{ \theta_1 } \sin \theta_1 - l_2 \dot{ \theta_2} \sin \theta_2


L=12m1l12θ1˙2+12m2(l1θ1˙cos⁡θ1+l2θ2˙cos⁡θ2)2+12m2(−l1θ1˙sin⁡θ1−l2θ2˙sin⁡θ2)2+m1gl1cos⁡θ1+m2g(l1cos⁡θ1+l2cos⁡θ2)\displaystyle \mathcal{ L} = \frac{1}{2} m_1 l_1^2 \dot{ \theta_1}^2 + \frac{1}{2} m_2 \left( l_1 \dot{ \theta_1 } \cos \theta_1 + l_2 \dot{ \theta_2} \cos \theta_2 \right)^2 + \frac{1}{2}m_2 \left(-l_1 \dot{ \theta_1 } \sin \theta_1 - l_2 \dot{ \theta_2} \sin \theta_2 \right)^2 + m_1 g l_1 \cos \theta_1 + m_2 g ( l_1 \cos \theta_1 + l_2 \cos \theta_2 )

=12m1l12θ1˙2+12m2l12θ1˙2+12m2l22θ2˙2+m2l1l2cos⁡(θ1−θ2)θ1˙θ2˙+m1gl1cos⁡θ1+m2g(l1cos⁡θ1+l2cos⁡θ2)\displaystyle = \frac{1}{2} m_1 l_1^2 \dot{ \theta_1}^2 + \frac{1}{2}m_2 l_1^2 \dot{\theta_1}^2 + \frac{1}{2}m_2l_2^2 \dot{\theta_2}^2 + m_2 l_1 l_2 \cos (\theta_1 - \theta_2 ) \dot{ \theta_1} \dot{ \theta_2} + m_1 g l_1 \cos \theta_1 + m_2 g ( l_1 \cos \theta_1 + l_2 \cos \theta_2 )

∂L∂θ1=−m2l1l2sin⁡(θ1−θ2)θ1˙θ2˙−m1gl1sin⁡θ1−m2gl1sin⁡θ1\displaystyle \frac{\partial \mathcal{ L}}{\partial \theta_1}= -m_2 l_1 l_2 \sin ( \theta_1 - \theta_2 ) \dot{ \theta_1} \dot{ \theta_2} - m_1 g l_1 \sin \theta_1 -m_2 g l_1 \sin \theta_1

≈−m2l1l2(θ1−θ2)θ1˙θ2˙−m1gl1θ1−m2gl1θ1\displaystyle \approx -m_2 l_1 l_2 ( \theta_1 - \theta_2 ) \dot{ \theta_1} \dot{ \theta_2} - m_1 g l_1 \theta_1 -m_2 g l_1 \theta_1

∂L∂θ1˙=m1l22θ1˙+m2l12θ1˙+m2l1l2cos⁡(θ1−θ2)θ2˙ \displaystyle \frac{\partial \mathcal{ L}}{\partial \dot{\theta_1}} =m_1 l_2^2 \dot{ \theta_1} + m_2 l_1^2 \dot{ \theta_1} + m_2 l_1 l_2 \cos ( \theta_1 - \theta_2 ) \dot{ \theta_2 }

ddt(∂L∂θ1˙)=m1l22θ1¨+m2l12θ1¨−(θ1˙−θ2˙)m2sin⁡(θ1−θ2)θ2˙+m2l1l2cos⁡(θ1−θ2)θ2¨\displaystyle \frac{d}{dt} \left( \frac{\partial \mathcal{ L}}{\partial \dot{\theta_1}}\right) = m_1 l_2^2 \ddot{ \theta_1} + m_2 l_1^2 \ddot{ \theta_1} - (\dot{\theta_1}- \dot{\theta_2} ) m_2 \sin (\theta_1-\theta_2 ) \dot{\theta_2} + m_2 l_1 l_2 \cos ( \theta_1 - \theta_2 ) \ddot{ \theta_2}

≈m1l22θ1¨+m2l12θ1¨−(θ1˙−θ2˙)m2(θ1−θ2)θ2˙+m2l1l2θ2¨\displaystyle \approx m_1 l_2^2 \ddot{ \theta_1} + m_2 l_1^2 \ddot{ \theta_1} - (\dot{\theta_1}- \dot{\theta_2} ) m_2 (\theta_1-\theta_2 ) \dot{\theta_2} + m_2 l_1 l_2 \ddot{ \theta_2}

ddt(∂L∂θ1˙)−∂L∂θ1=0\displaystyle \frac{d}{dt} \left( \frac{\partial \mathcal{ L}}{\partial \dot{\theta_1}}\right) - \frac{\partial \mathcal{ L}}{\partial \theta_1} = 0

m1l22θ1¨+m2l12θ1¨−(θ1˙−θ2˙)m2(θ1−θ2)θ2˙+m2l1l2θ2¨+m2l1l2(θ1−θ2)θ1˙θ2˙+m1gl1θ1+m2gl1θ1=0\displaystyle m_1 l_2^2 \ddot{ \theta_1} + m_2 l_1^2 \ddot{ \theta_1} - (\dot{\theta_1}- \dot{\theta_2} ) m_2 (\theta_1-\theta_2 )\dot{\theta_2} + m_2 l_1 l_2 \ddot{ \theta_2} +m_2 l_1 l_2 ( \theta_1 - \theta_2 ) \dot{ \theta_1} \dot{ \theta_2} + m_1 g l_1 \theta_1 +m_2 g l_1 \theta_1 =0

m1l22θ1¨+m2l12θ1¨−(θ1˙θ2˙−θ2˙2)m2(θ1−θ2)+m2l1l2θ2¨+m2l1l2θ1θ1˙θ2˙−m2l1l2θ2θ1˙θ2˙+m1gl1θ1+m2gl1θ1=0\displaystyle m_1 l_2^2 \ddot{ \theta_1} + m_2 l_1^2 \ddot{ \theta_1} - (\dot{\theta_1}\dot{\theta_2}- \dot{\theta_2}^2 ) m_2 (\theta_1-\theta_2 ) + m_2 l_1 l_2 \ddot{ \theta_2} +m_2 l_1 l_2 \theta_1 \dot{ \theta_1} \dot{ \theta_2} - m_2 l_1 l_2 \theta_2 \dot{ \theta_1} \dot{ \theta_2} + m_1 g l_1 \theta_1 +m_2 g l_1 \theta_1 =0

m1l22θ1¨+m2l12θ1¨−θ1θ1˙θ2˙m2l1l2+θ1˙θ2˙θ2m2l1l2+θ2˙2θ1m1l1l2−θ2˙2θ2m2l1l2+m2l1l2θ2¨+m2l1l2θ1θ1˙θ2˙−m2l1l2θ2θ1˙θ2˙+m1gl1θ1+m2gl1θ1=0\displaystyle m_1 l_2^2 \ddot{ \theta_1} + m_2 l_1^2 \ddot{ \theta_1} - \theta_1 \dot{\theta_1 } \dot{\theta_2} m_2 l_1 l_2 + \dot{\theta_1} \dot{\theta_2}\theta_2 m_2 l_1 l_2 + \dot{\theta_2}^2 \theta_1 m_1 l_1 l_2 - \dot{\theta_2}^2 \theta_2 m_2 l_1 l_2 + m_2 l_1 l_2 \ddot{ \theta_2} +m_2 l_1 l_2 \theta_1 \dot{ \theta_1} \dot{ \theta_2} - m_2 l_1 l_2 \theta_2 \dot{ \theta_1} \dot{ \theta_2} + m_1 g l_1 \theta_1 +m_2 g l_1 \theta_1 =0

m1l22θ1¨+m2l12θ1¨+θ2˙2θ1m1l1l2−θ2˙2θ2m2l1l2+m2l1l2θ2¨+m1gl1θ1+m2gl1θ1=0\displaystyle m_1 l_2^2 \ddot{ \theta_1} + m_2 l_1^2 \ddot{ \theta_1} + \dot{\theta_2}^2 \theta_1 m_1 l_1 l_2 - \dot{\theta_2}^2 \theta_2 m_2 l_1 l_2 + m_2 l_1 l_2 \ddot{ \theta_2} + m_1 g l_1 \theta_1 +m_2 g l_1 \theta_1 =0

Ignoring none linear terms.

m1l22θ1¨+m2l12θ1¨+m2l1l2θ2¨+m1gl1θ1+m2gl1θ1=0\displaystyle m_1 l_2^2 \ddot{ \theta_1} + m_2 l_1^2 \ddot{ \theta_1} + m_2 l_1 l_2 \ddot{ \theta_2} + m_1 g l_1 \theta_1 +m_2 g l_1 \theta_1 =0

∂L∂θ2=m2l1l2sin⁡(θ1−θ2)θ1˙θ2˙−m2gl2sin⁡θ2 \displaystyle \frac{\partial \mathcal{ L}}{\partial \theta_2} = m_2 l_1 l_2 \sin ( \theta_1 - \theta_2 ) \dot{\theta_1} \dot{ \theta_2} - m_2 g l_2 \sin \theta_2

≈m2l1l2(θ1−θ2)θ1˙θ2˙−m2gl2θ2 \displaystyle \approx m_2 l_1 l_2 ( \theta_1 - \theta_2 ) \dot{\theta_1} \dot{ \theta_2} - m_2 g l_2 \theta_2

∂L∂θ2˙=m2l22θ2˙+m2l1l2cos⁡(θ1−θ2)θ1˙\displaystyle \frac{\partial \mathcal{ L}}{\partial \dot{\theta_2}}= m_2 l_2^2 \dot{\theta_2 } + m_2 l_1 l_2 \cos ( \theta_1 - \theta_2 ) \dot{ \theta_1}

ddt(∂L∂θ1˙)=m2l22θ2¨−(θ1˙−θ2˙)m2l1l2sin⁡(θ1−θ2)θ1˙+m2l1l2cos⁡(θ1−θ2)θ1¨\displaystyle \frac{d}{dt} \left( \frac{\partial \mathcal{ L}}{\partial \dot{\theta_1}}\right) = m_2 l_2^2 \ddot{\theta_2} - (\dot{\theta_1} - \dot{\theta_2} )m_2 l_1 l_2 \sin ( \theta_1 - \theta_2 ) \dot{ \theta_1} + m_2 l_1 l_2 \cos (\theta_1 - \theta_2 ) \ddot{ \theta_1}

≈m2l22θ2¨−(θ1˙−θ2˙)m2l1l2(θ1−θ2)θ1˙+m2l1l2θ1¨\displaystyle \approx m_2 l_2^2 \ddot{\theta_2} - (\dot{\theta_1} - \dot{\theta_2} )m_2 l_1 l_2 ( \theta_1 - \theta_2 ) \dot{ \theta_1} + m_2 l_1 l_2 \ddot{ \theta_1}

ddt(∂L∂θ2˙)−∂L∂θ2=0\displaystyle \frac{d}{dt} \left( \frac{\partial \mathcal{ L}}{\partial \dot{\theta_2}}\right) - \frac{\partial \mathcal{ L}}{\partial \theta_2} = 0

m2l22θ2¨−(θ1˙−θ2˙)m2l1l2(θ1−θ2)θ1˙+m2l1l2θ1¨−m2l1l2(θ1−θ2)θ1˙θ2˙+m2gl2θ2=0 \displaystyle m_2 l_2^2 \ddot{\theta_2} - (\dot{\theta_1} - \dot{\theta_2} )m_2 l_1 l_2 ( \theta_1 - \theta_2 ) \dot{ \theta_1} + m_2 l_1 l_2 \ddot{ \theta_1} -m_2 l_1 l_2 ( \theta_1 - \theta_2 ) \dot{\theta_1} \dot{ \theta_2} + m_2 g l_2 \theta_2 =0

Ignoring non linear terms.

m2l22θ2¨+m2l1l2theta1¨=−m2gl2θ2 m_2l_2^2 \ddot{\theta_2} + m_2 l_1 l_2 \ddot{theta_1} = -m_2gl_2 \theta_2

We have

l12(m1+m2)θ1¨+l1l2m2θ2¨=gl1(m1+m2)θ1\displaystyle {l_1} ^2(m_1 +m_2) \ddot{\theta_1} + l_1 l_2 m_2 \ddot{\theta_2} = gl_1 (m_1 +m_2 ) \theta_1

and

m2l22θ2¨+m2l1l2theta1¨=−m2gl2θ2 m_2l_2^2 \ddot{\theta_2} + m_2 l_1 l_2 \ddot{theta_1} = -m_2gl_2 \theta_2

So;

MΘ¨=−KΘM \ddot{\Theta} = -K \Theta where,

M=(l12(m1+m2)l1l2m2l1l2m2l22m2)M= \begin{pmatrix} {l_1} ^2(m_1 +m_2) & l_1 l_2 m_2 \\l_1 l_2 m_2 & {l_2} ^2 m_2 \end{pmatrix}

K=(gl1(m1+m2)00gl2m2) K = \begin{pmatrix} gl_1 (m_1 +m_2) & 0 \\ 0 & gl_2 m_2 \end{pmatrix}

and Θ=(θ1θ2) \Theta = \begin{pmatrix} \theta_1 \\ \theta_2 \end{pmatrix}


Beaten :colonhash: was planning to type this later :colonhash:
Original post by cpdavis
Beaten :colonhash: was planning to type this later :colonhash:


Sorry :tongue: Although I think I may have done you a favor, it took and hour and a half to type that. :pierre:

Quick Reply

Related discussions

Latest

Trending

Trending

Articles for you