The Proof is Trivial!
Scroll to see replies
Original post by und
Solution 50
Using as the initial velocity.
Since the function of is continuous, if for some , then at that instant the frictional force must be greater than the weight, thus the rope will remain stationery. It remains to find a range of values of for which will become .
Creating and solving the differential equation, we obtain , so if is to be for some positive , then there must exist a positive root , so a necessary and sufficient condition (assuming all the constant terms are positive) is as required.
If the rope has mass , then the impulse applied to accelerate the rope to a speed is given by the change of momentum . Hence , giving the maximum impulse as .
Using as the initial velocity.
Since the function of is continuous, if for some , then at that instant the frictional force must be greater than the weight, thus the rope will remain stationery. It remains to find a range of values of for which will become .
Creating and solving the differential equation, we obtain , so if is to be for some positive , then there must exist a positive root , so a necessary and sufficient condition (assuming all the constant terms are positive) is as required.
If the rope has mass , then the impulse applied to accelerate the rope to a speed is given by the change of momentum . Hence , giving the maximum impulse as .
I think this is the most natural solution to the question. But it is very STEP-esque to have multiple possible solutions.
Original post by und
Sorry to be blunt but this is all rather unconvincing. Consider what happens if we decide to make theta smaller. We can then increase ab.
I said that if you increase the side length of 3, then the other side can becomes at most 3. This means that you have this new side of length 3 and the old one of length 2. If you increase the one of length 2 the other side must become at most 2, hence you still have sides of at most length 3 and 2. If you increase both then you have sides lengths of at most 2, just over 3 and just over 3. But you can have side lengths of 2 and 3 and one larger so this still gives the most area as the area depends only on the two sides 2 and 3 and the angle between them.
If it wasn't clear enough in my original post I am editing it now.
Edit: I'll admit that my original post didn't have the best explanation, but the idea was there that you couldn't get longer shortest side lengths than of 2 and 3.
(edited 11 years ago)
Problem 56 **/***
Evaluate
Evaluate
(edited 11 years ago)
Original post by metaltron
I said that if you increase the side length of 3, then the other side can becomes at most 3. This means that you have this new side of length 3 and the old one of length 2. If you increase the one of length 2 the other side must become at most 2, hence you still have sides of at most length 3 and 2. If you increase both then you have sides lengths of at most 2, just over 3 and just over 3. But you can have side lengths of 2 and 3 and one larger so this still gives the most area as the area depends only on the two sides 2 and 3 and the angle between them.
If it wasn't clear enough in my original post I am editing it now.
Edit: I'll admit that my original post didn't have the best explanation, but the idea was there that you couldn't get longer shortest side lengths than of 2 and 3.
If it wasn't clear enough in my original post I am editing it now.
Edit: I'll admit that my original post didn't have the best explanation, but the idea was there that you couldn't get longer shortest side lengths than of 2 and 3.
I see what you mean, but it could have been explained better in the solution. So your argument is as follows if I understood correctly.
Spoiler
I'm very disappointed I never gave this question greater thought in the actual exam. This is a nice solution.
(edited 11 years ago)
Original post by Indeterminate
Problem 56 ***
Evaluate
Evaluate
Isn't there a really easy way of doing this, only needing A-Level knowledge? (Don't read the spoiler if you want to do the question)
Spoiler
Original post by und
I see what you mean, but it could have been explained better in the solution. So your argument is as follows if I understood correctly.
I'm very disappointed I never gave this question greater thought in the actual exam. This is a nice solution.
Spoiler
I'm very disappointed I never gave this question greater thought in the actual exam. This is a nice solution.
Yeah that's it! It's a really easy question if you can word your answer right, but for some reason in that exam I had so many mental blocks. Was pretty upset after that paper, especially since it was the easiest in ages. Anyway, bring on next year's!
Original post by und
I see what you mean, but it could have been explained better in the solution. So your argument is as follows if I understood correctly.
I'm very disappointed I never gave this question greater thought in the actual exam. This is a nice solution.
Spoiler
I'm very disappointed I never gave this question greater thought in the actual exam. This is a nice solution.
The better way of explaining this I think is once you get to the formula for the area, to say something like:
"We cannot use a side of length 4 as one of the legs of the triangle, as the hypotenuse would be larger than 4, which isn't allowed. Thus take the legs of the triangle to be 2 and 3; by Pythagoras, the hypotenuse is 3^2 + 2^2 = 13 < 4^2 (so satisfies the restrictions). Hence the maximum area of the triangle is (1/2)*2*3=3."
(This is obviously the same as what you've written, except I think you should make the point about the a leg of length 4 explicit.)
Are all BMO1 problems this short?
(edited 11 years ago)
Original post by shamika
The better way of explaining this I think is once you get to the formula for the area, to say something like:
"We cannot use a side of length 4 as one of the legs of the triangle, as the hypotenuse would be larger than 4, which isn't allowed. Thus take the legs of the triangle to be 2 and 3; by Pythagoras, the hypotenuse is 3^2 + 2^2 = 13 < 4^2 (so satisfies the restrictions). Hence the maximum area of the triangle is (1/2)*2*3=3."
Are all BMO1 problems this short?
"We cannot use a side of length 4 as one of the legs of the triangle, as the hypotenuse would be larger than 4, which isn't allowed. Thus take the legs of the triangle to be 2 and 3; by Pythagoras, the hypotenuse is 3^2 + 2^2 = 13 < 4^2 (so satisfies the restrictions). Hence the maximum area of the triangle is (1/2)*2*3=3."
Are all BMO1 problems this short?
Isn't it OK simply to consider the two shorter sides which are less than 2 and 3 respectively?
This year the paper was much easier than usual. The only reasonably difficult question was Q6 - I wasted a lot of time trying to solve that one without any success.
Original post by shamika
The better way of explaining this I think is once you get to the formula for the area, to say something like:
"We cannot use a side of length 4 as one of the legs of the triangle, as the hypotenuse would be larger than 4, which isn't allowed. Thus take the legs of the triangle to be 2 and 3; by Pythagoras, the hypotenuse is 3^2 + 2^2 = 13 < 4^2 (so satisfies the restrictions). Hence the maximum area of the triangle is (1/2)*2*3=3."
(This is obviously the same as what you've written, except I think you should make the point about the a leg of length 4 explicit.)
Are all BMO1 problems this short?
"We cannot use a side of length 4 as one of the legs of the triangle, as the hypotenuse would be larger than 4, which isn't allowed. Thus take the legs of the triangle to be 2 and 3; by Pythagoras, the hypotenuse is 3^2 + 2^2 = 13 < 4^2 (so satisfies the restrictions). Hence the maximum area of the triangle is (1/2)*2*3=3."
(This is obviously the same as what you've written, except I think you should make the point about the a leg of length 4 explicit.)
Are all BMO1 problems this short?
The completing the square one was even shorter surely?
Original post by shamika
Isn't there a really easy way of doing this, only needing A-Level knowledge? (Don't read the spoiler if you want to do the question)
Spoiler
Spoiler
(Almost complete) Solution 27
This representation is all well and good, but as noted by my earlier attempts, any attempt to evaluate in any coordinate system with the integrand in this form leads to a very cumbersome/impossible integral. The aim is thus to represent it in an equivalent form that will make the integration easier.
Notice that if are the vectors such that , then:
If we take the unit vector in the direction of and call it , then
. In order to be able to express any point in , we need two more unit vectors which are all perpendicular to each other, say . As the three vectors are mutually orthogonal and of unit length in their directions, then they can now form an alternative way of expressing points in and so form an orthonormal basis.
Let these three unit vectors have associated coordinates . Then since they are orthonormal, the region we are integrating over can still be written in the same form, just with the coordinates substituted for . In our new orthonormal basis:
and so we can rewrite as:
, with the region in that we are integrating over defined by . However, this could be potentially a troublesome integral because of the limits and so this integral would better be evaluated in the spherical coordinate system rather than the cartesian. So changing the variables over redefines the region in that we are integrating over as , multiplying by the Jacobian and picking our order of integrating carefully so as not to run into trouble gives:
One iteration of integration by parts gives
The second part of this question is still to be completed.
This representation is all well and good, but as noted by my earlier attempts, any attempt to evaluate in any coordinate system with the integrand in this form leads to a very cumbersome/impossible integral. The aim is thus to represent it in an equivalent form that will make the integration easier.
Notice that if are the vectors such that , then:
If we take the unit vector in the direction of and call it , then
. In order to be able to express any point in , we need two more unit vectors which are all perpendicular to each other, say . As the three vectors are mutually orthogonal and of unit length in their directions, then they can now form an alternative way of expressing points in and so form an orthonormal basis.
Let these three unit vectors have associated coordinates . Then since they are orthonormal, the region we are integrating over can still be written in the same form, just with the coordinates substituted for . In our new orthonormal basis:
and so we can rewrite as:
, with the region in that we are integrating over defined by . However, this could be potentially a troublesome integral because of the limits and so this integral would better be evaluated in the spherical coordinate system rather than the cartesian. So changing the variables over redefines the region in that we are integrating over as , multiplying by the Jacobian and picking our order of integrating carefully so as not to run into trouble gives:
One iteration of integration by parts gives
The second part of this question is still to be completed.
(edited 11 years ago)
Original post by DJMayes
No, that's fair enough. I tend to opt for Differential Equations because I like transforming a Mechanics question into a Pure question (And one of the nicer Pure topics in my opinion) but some of the energy solutions are really nice.
Yeah - DEs can give really neat solutions for mechanics questions, e.g. SHM.

Solution 57
Let the integral be . Apply to get (by the oddity of tan), then add the two forms of together and divide by 2 to obtain .
Let the integral be . Apply to get (by the oddity of tan), then add the two forms of together and divide by 2 to obtain .
Original post by Farhan.Hanif93
Solution 57
Let the integral be . Apply to get (by the oddity of tan), then add the two forms of together and divide by 2 to obtain .
Let the integral be . Apply to get (by the oddity of tan), then add the two forms of together and divide by 2 to obtain .
Nice, my method was to split it into 2 integrals, 1/(1+x^2) and another where the integrand was odd so it went to 0.
Original post by Farhan.Hanif93
Solution 57
Let the integral be . Apply to get (by the oddity of tan), then add the two forms of together and divide by 2 to obtain .
Let the integral be . Apply to get (by the oddity of tan), then add the two forms of together and divide by 2 to obtain .
Damn beat me to it :/
Well I guess I'll provide another physicsy mathsy problem 
Problem 58 **/***
A double pendulum consists of a mass m2 suspended by a rod of length l2 from a mass m1, which is itself suspended by a rod of length l1 from a fixed pivot, as shown below.
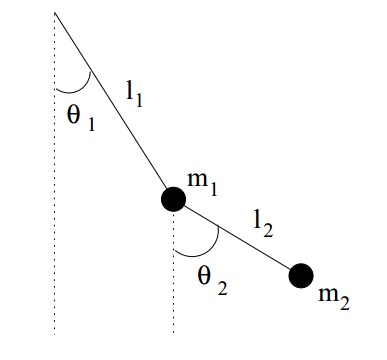
Show that the equations of motion for small displacements can be written as
where,
and

Problem 58 **/***
A double pendulum consists of a mass m2 suspended by a rod of length l2 from a mass m1, which is itself suspended by a rod of length l1 from a fixed pivot, as shown below.
Show that the equations of motion for small displacements can be written as
where,
and
Hint for 56:
Consider the integral
with the substitution
Residue theorem!
Consider the integral
with the substitution
Residue theorem!

Quick Reply
Related discussions
- Proof by induction - general question - why prove n=1 works?
- I am the biggest ****** in the world, please remind me ocassionally in case I forget
- Proof question
- BMO 1993, Round 1, Question 3
- Discrete maths questions
- A level maths proof Q
- How should I go about preparing for the STEP Maths exam?
- Range of a function
- PDEs
- AI in robotics PS?
- CV going into Uni
- The hard grade 9 maths questions thread 2023
- How to practice GCSE OCR Computer Science J277 Paper 2?
- Procrastination
- English language paper 2 exam !!
- OCR a level exam question
- Demoivres theorem quick application
- Is there a rule of thumb of when to use integration by parts or substitution?
- How would the mass at B work in this moments question?
- Job offer won't accept my proof of address
Latest
Last reply 1 minute ago
UAL Bsc Fashion Management and fashion marketingLast reply 2 minutes ago
LSE anthropology and law 2024Last reply 2 minutes ago
Medical doctor degree apprenticeship 2024Last reply 2 minutes ago
Official London School of Economics and Political Science 2024 Applicant ThreadPosted 5 minutes ago
UNIT 7 ASSIGNMENT 2 D3 AND 4 (health and social care)Last reply 7 minutes ago
LSE International Social and Public Policy and Economics (LLK1) 2024 ThreadLast reply 7 minutes ago
JK Rowling in ‘arrest me’ challenge over hate crime lawLast reply 7 minutes ago
Official: Queen's University Belfast A100 2024 Entry ApplicantsLast reply 10 minutes ago
Official Durham University Offer Holders Thread for 2024 entryLast reply 10 minutes ago
Accenture Degree Apprenticeship 2024Last reply 11 minutes ago
What would you say to someone struggling with severe anxiety?Last reply 23 minutes ago
Children to no longer be prescribed puberty blockers, NHS England confirmsLast reply 24 minutes ago
Edexcel A Level Economics A Paper 1 (9ECO 01) - 15th May 2024 [Exam Chat]Last reply 24 minutes ago
Official: University of Manchester A106 2024 Entry ApplicantsMedical Schools
1274
Last reply 25 minutes ago
LSE accommodation Q and ALast reply 25 minutes ago
Amazon Project management apprenticeship 2024Last reply 26 minutes ago
OCR A-level English Literature Paper 1 (H472/01) - 24th May 2024 [Exam Chat]Trending
Last reply 1 week ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71
Trending
Last reply 1 week ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71



