What's your favourite proof in maths?

Inspired by the favourite number thread. Feel free to sketch up the details of the proof if you wish to. It doesn't have to be your favourite proof of a main theorem or result. It could be the proof or calculation of some simple equation, or even some cool method that you have seen somewhere (your book etc). For example, deriving the quadratic formula by completing the square. I'll start.

Gauss' derivation of the sum of first n natural numbers.

Let S be the sum. Then

S = 1+2+3+....+(n-1)+n ---------------- (1)

But writing it from the other side

S = n+(n-1)+(n-2)+...+2+1 -------- (2)

Adding (1) and (2) together

2S = n(n+1)

So S = [n(n+1)]/2. :drool:

(edited 10 years ago)

Scroll to see replies

Reply 1

the bear

Euclid's proof of the infinitude of primes... it is brilliant, yet simple enough for a Higher Level GCSE child to understand.

http://www.math.utah.edu/~pa/math/q2.html

(edited 10 years ago)

Reply 2

ThePerfectScore

Original post by the bear

Euclid's proof of the infinitude of primes... it is brilliant, yet simple enough for a Higher Level GCSE child to understand.

http://www.math.utah.edu/~pa/math/q2.html

Euclid was a clever man! :biggrin:

Way ahead of his time! :eek:

Reply 3

the bear

Original post by ThePerfectScore

Euclid was a clever man! :biggrin:

Way ahead of his time! :eek:

indeed. he has brought pleasure to untold millions of school children.

Reply 4

Noble.

- Fundamental theorem of algebra via Liouville's theorem
- Sub-additivity of the Lebesgue measure by constructing pairwise disjoint sets
- Proving any open subset of

\mathbb{R}

is the union of, at most, countably many disjoint, open intervals via defining an equivalence relation.

I don't really keep an ongoing list of favourite proofs, but the above are a few recent proofs I've seen that stand out as being particularly neat.

Reply 5

interstitial

Proof that

\sqrt k

is irrational when

\sqrt{k} \not\in \mathbb N

, but

k \in \mathbb N

Gotta love that infinite descent :teehee:

And also the proof that

\displaystyle\sum_{r=1}^\infty \dfrac{1}{r^2} = \dfrac{\pi ^2}{6}

Posted from TSR Mobile

(edited 10 years ago)

Reply 6

FireGarden

I have a fair few proofs I'm very fond of, but here's a real nice one:

Theorem: There exist two positive irrationals

x,y

such that

x^y

is rational.

Proof: If

\sqrt{2}^{\sqrt{2}}

is rational, take

x=y=\sqrt{2}

.

If

\sqrt{2}^{\sqrt{2}}

is irrational, take

x=\sqrt{2}^{\sqrt{2}},\ y=\sqrt{2}

.

Another theorem, whose proof once came with advice from the lecturer: "You need to be able to write this proof in the snow with pee even at night when drunk"

There is no surjection

:A\mapsto \mathcal{P}(A)

Reply 7

Hodor

The proof that the real numbers are uncountable, using Baire's theorem:

Write

\mathbb{R} = \bigcup\limits_{x \in \mathbb{R}} \{x\}

. For each

x

\{x\}

is closed in

\mathbb{R}

and has empty interior, so, since

\mathbb{R}

is a complete metric space, Baire says that the union cannot be countable.

Reply 8

JPL9457

(edited 10 years ago)

Reply 9

interstitial

Original post by JPL9457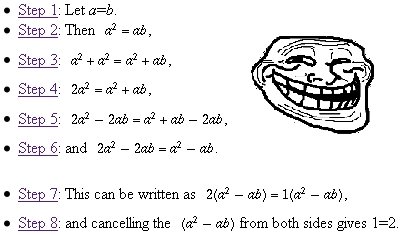

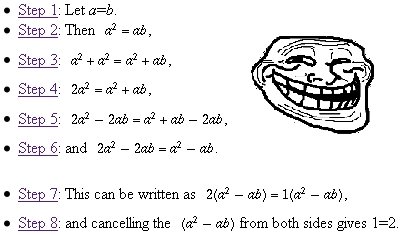
Division by zero :hand:

This may have worked somewhere else, but this is the maths thread where people actually know about maths :tongue:

Posted from TSR Mobile

Reply 10

You Failed

Original post by majmuh24

Division by zero :hand:

This may have worked somewhere else, but this is the maths thread where people actually know about maths :tongue:

Posted from TSR Mobile

I'm pretty sure he was taking the piss, hence the massive troll face.

Reply 11

thewagwag

Cantor's diagonal argument. Proof that there are infinities of different sizes, by showing how there must be more real numbers than whole numbers, despite both sets being infinite

Posted from TSR Mobile

Reply 12

username1258398

Original post by thewagwag

Cantor's diagonal argument. Proof that there are infinities of different sizes, by showing how there must be more real numbers than whole numbers, despite both sets being infinite

I second this! :biggrin:

Such an original, simple line of thought. Makes you wonder how in the banana he came up with it.

Reply 13

JPL9457

Original post by majmuh24

Division by zero :hand:

This may have worked somewhere else, but this is the maths thread where people actually know about maths :tongue:

Posted from TSR Mobile

erm i'll have you know i got a 5 in my maths SAT, i am a very capable mathematician

Reply 14

Autistic Merit

Original post by JPL9457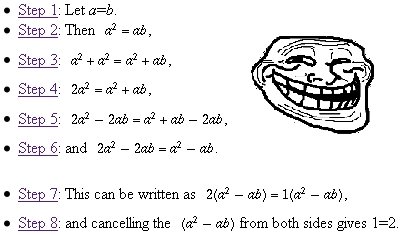

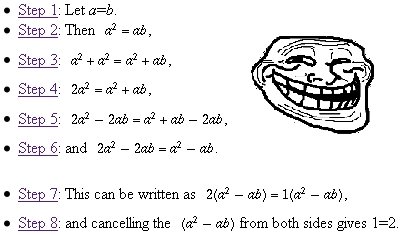
Not going to lie, I graduated with a first in maths but have no idea how I would go about contradicting this proof.

Reply 15

interstitial

Original post by You Failed

I'm pretty sure he was taking the piss, hence the massive troll face.

I know, I was joking :wink:

Original post by JPL9457

erm i'll have you know i got a 5 in my maths SAT, i am a very capable mathematician

I only got a level 4, does that make me stupid (I got a level 3 in Year 2 though :redface:

)

Posted from TSR Mobile

Reply 16

Doglamlico

Original post by majmuh24

Proof that

\sqrt k

is irrational when

k > 0

and

\sqrt{k} \not\in \mathbb N

Gotta love that infinite descent :teehee:

What?

k=\frac{1}{4} > 0 \\\sqrt{k}=\frac{1}{2}\not\in \mathbb N

Reply 17

interstitial

Original post by StrangeBanana

I second this! :biggrin:

Such an original, simple line of thought. Makes you wonder how in the banana he came up with it.

His theorem about power sets was also so simple, yet so obvious, it extended infinities beyond the simple 1,2,3,4.. and gave rise to uncountable infinities as well :redface:

His continuum hypothesis is pretty interesting as well :wink:

Posted from TSR Mobile