Cubic equations - determining the nature of roots
Hi so I've been working on the Oxford uni maths bridging material and was wondering if there is a simpler way to determine the nature of roots of a standard cubic
I know that a discriminant exists for cubics,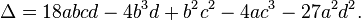
but this seems tricky to remember and I believe it would be better to ''understand'' why this formula is true, or use graphs, turning points etc to determine the nature of roots (if that is possible)
tl;dr can someone tell me how I'd go about proving this discriminant or how I'd use other methods to determine the natural of roots of a polynomial like x^3+px+q=0
I know that a discriminant exists for cubics,
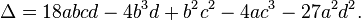
but this seems tricky to remember and I believe it would be better to ''understand'' why this formula is true, or use graphs, turning points etc to determine the nature of roots (if that is possible)
tl;dr can someone tell me how I'd go about proving this discriminant or how I'd use other methods to determine the natural of roots of a polynomial like x^3+px+q=0
Original post by plusC
tl;dr can someone tell me how I'd go about proving this discriminant or how I'd use other methods to determine the natural of roots of a polynomial like x^3+px+q=0
tl;dr can someone tell me how I'd go about proving this discriminant or how I'd use other methods to determine the natural of roots of a polynomial like x^3+px+q=0
In this case you have a depressed cubic. You can solve it using the identity .
You can use a substitution of the form x=X-A to transform any cubic equation into a depressed cubic.
For example can be transformed into using the substitution .
On the other hand, I don't think anyone expects you to memorise the discriminant. If you ever need it you can look it up.
Original post by BabyMaths
In this case you have a depressed cubic. You can solve it using the identity .
You can use a substitution of the form x=X-A to transform any cubic equation into a depressed cubic.
For example can be transformed into using the substitution .
On the other hand, I don't think anyone expects you to memorise the discriminant. If you ever need it you can look it up.
You can use a substitution of the form x=X-A to transform any cubic equation into a depressed cubic.
For example can be transformed into using the substitution .
On the other hand, I don't think anyone expects you to memorise the discriminant. If you ever need it you can look it up.
Oh I see and from here -3yz=p and q=y^3+z^3 yes? and then presumably I can use these to find the values of y and z in terms of p and q (or do I need more?)
Apart from that useful tip, how would I determine the nature of roots of a depressed cubic, take the discriminant of the quadratic formed and compare it to the other factor? or use the formula obviously
Original post by plusC
Oh I see and from here -3yz=p and q=y^3+z^3 yes? and then presumably I can use these to find the values of y and z in terms of p and q (or do I need more?)
Apart from that useful tip, how would I determine the nature of roots of a depressed cubic, take the discriminant of the quadratic formed and compare it to the other factor? or use the formula obviously
Apart from that useful tip, how would I determine the nature of roots of a depressed cubic, take the discriminant of the quadratic formed and compare it to the other factor? or use the formula obviously
You could also think about stationary points.
Original post by BabyMaths
You could also think about stationary points.
And lastly say if you calculated some stationary points but the solution to dy/dx=0 was actually imaginary e.g. x^2=-p/3 for p>0 which yields imaginary solutions, how would you then determine the number of roots the cubic has if its turning points aren't real? thanks
Original post by plusC
And lastly say if you calculated some stationary points but the solution to dy/dx=0 was actually imaginary e.g. x^2=-p/3 for p>0 which yields imaginary solutions, how would you then determine the number of roots the cubic has if its turning points aren't real? thanks
I've been assuming that your a,b,c and d are real.
If there's no real x such that dy/dx=0 what does the graph of y=ax^3+bx^2+cx+d look like?
How many real roots are there then? How many complex roots?
Original post by BabyMaths
I've been assuming that your a,b,c and d are real.
If there's no real x such that dy/dx=0 what does the graph of y=ax^3+bx^2+cx+d look like?
How many real roots are there then? How many complex roots?
If there's no real x such that dy/dx=0 what does the graph of y=ax^3+bx^2+cx+d look like?
How many real roots are there then? How many complex roots?
Yeah they are real, I'm not quite sure but if it doesn't turn would it be like a curvy straight line, or are there points of inflexion to consider
I'm going to take a guess and say a complex conjugate and one real root (there must be at least one real solution so crosses an axis once but never turns)
Is this right?
Original post by plusC
Is this right?
Yes.
Original post by plusC
Hi so I've been working on the Oxford uni maths bridging material and was wondering if there is a simpler way to determine the nature of roots of a standard cubic
I know that a discriminant exists for cubics,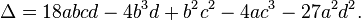
but this seems tricky to remember and I believe it would be better to ''understand'' why this formula is true, or use graphs, turning points etc to determine the nature of roots (if that is possible)
tl;dr can someone tell me how I'd go about proving this discriminant or how I'd use other methods to determine the natural of roots of a polynomial like x^3+px+q=0
I know that a discriminant exists for cubics,
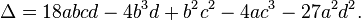
but this seems tricky to remember and I believe it would be better to ''understand'' why this formula is true, or use graphs, turning points etc to determine the nature of roots (if that is possible)
tl;dr can someone tell me how I'd go about proving this discriminant or how I'd use other methods to determine the natural of roots of a polynomial like x^3+px+q=0
If you've eliminated the x^2 term by a translation, then the discriminant is a lot easier to remember and for such a cubic is easy to derive by looking at where the cubic's stationary points are (in relation to the x-axis)..
Another method of solution though - for such a depressed cubic - is to substitute in x = k cos(t) where k is chosen so that the resulting expression in a multiple of cos(3t). This method works fine for complex roots as well provided you know a little about the complex trig functions.
What bridging material are you using by the way?
Original post by RichE
If you've eliminated the x^2 term by a translation, then the discriminant is a lot easier to remember and for such a cubic is easy to derive by looking at where the cubic's stationary points are (in relation to the x-axis)..
Another method of solution though - for such a depressed cubic - is to substitute in x = k cos(t) where k is chosen so that the resulting expression in a multiple of cos(3t). This method works fine for complex roots as well provided you know a little about the complex trig functions.
What bridging material are you using by the way?
Another method of solution though - for such a depressed cubic - is to substitute in x = k cos(t) where k is chosen so that the resulting expression in a multiple of cos(3t). This method works fine for complex roots as well provided you know a little about the complex trig functions.
What bridging material are you using by the way?
Oh interesting alternate method - will be sure to keep it in mind and try it out later, I'm using this:
https://www.maths.ox.ac.uk/prospective-students/undergraduate/background quite interesting and helpful
Quick Reply
Related discussions
- Edexcel alevel maths question
- Can anyone answer this GCSE cubic graph question??
- One cubic root is reciprocal of other question
- A level pure maths question
- Simple differentiation question
- is it just me or is this question incomplete??
- Habs Boys 16+ Entry 2023
- Edexcel Maths AS Pure June 2023 Q1(b)
- Further maths core pure roots of polynomials question.
- P1 How do I find part b?
- A-level Maths Question
- Can someone please help me with this question? A level further maths
- Math help - factorising cubic equations
- Maths Question Help Please
- I think I have done some dodgy algebra (parametrics a level maths)
- Oxbridge Maths - Interview Questions
- Analytical analysis
- Finding values of k for two distinct real roots
- Integral calculus
- Edexcel A-level Further Mathematics Paper 2 (9FM0 02) - 5th June 2023 [Exam Chat]
Latest
Last reply 1 minute ago
CPS Pupillage/Legal Trainee Scheme 2024 (2025 Start)Last reply 1 minute ago
Official Dental Hygiene and Therapy (Oral Health Science) 2024 Entry ThreadDentistry
2917
Last reply 1 minute ago
Official University of Bristol Applicant Thread for 2024Last reply 1 minute ago
Official London School of Economics and Political Science 2024 Applicant ThreadLast reply 3 minutes ago
Official UCL Offer Holders Thread for 2024 entryLast reply 5 minutes ago
Official University of Warwick Offer Holders Thread for 2024 entryLast reply 5 minutes ago
Amazon Project management apprenticeship 2024Last reply 7 minutes ago
Official: Queen's University Belfast A100 2024 Entry ApplicantsLast reply 12 minutes ago
which unis will accept BBB for economicsTrending
Last reply 20 hours ago
Did Cambridge maths students find maths and further maths a level very easy?Last reply 2 weeks ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71
Trending
Last reply 20 hours ago
Did Cambridge maths students find maths and further maths a level very easy?Last reply 2 weeks ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71



