Geometrical constructions (really fun[not a lie])
I have a lot of geometrical construction problems I can't do so I thought I'd make a thread of them.
Well, the first one's just your good old isosocles rectangular traingular, but I included it because it's probably a hint on how to do the others. I've found a few ways of doing the second but they all need Euclid's construction to multiply out a factor of root 2, and I can't see a way of generalizing it to the last bit, although I've been told it's "trivial". So I was wondering if there's a nicer way.
My way:
I don't have time to get a picture and explain what I've done so far with these 'cause I have a lecture.
Give geometrical constructions for
Well, the first one's just your good old isosocles rectangular traingular, but I included it because it's probably a hint on how to do the others. I've found a few ways of doing the second but they all need Euclid's construction to multiply out a factor of root 2, and I can't see a way of generalizing it to the last bit, although I've been told it's "trivial". So I was wondering if there's a nicer way.
My way:
Spoiler
I don't have time to get a picture and explain what I've done so far with these 'cause I have a lecture.
Spoiler

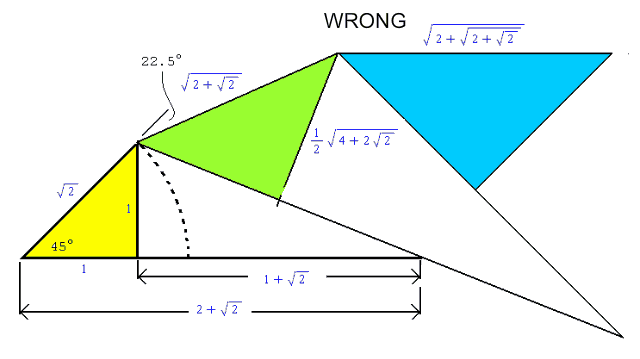
I think is the construction Hardy was looking for. Draw the first 45-45-90 triangle with a hypotenuse of sqrt(2) as shown in yellow. Then, using a compass, measure the sqrt(2) amount to the baseline, and add 2 more to that to get a triangle of base 2+sqrt(2). Then you can subtract 1 from 2+sqrt(2) to get the base measurement of another right triangle, which by the Pythagorean theorem has a hypotenuse of sqrt(4+2*sqrt(2)). Divide this new hypotenuse in half and build another 45-45-90 triangle with two sides of length (½)*sqrt(4+2*sqrt(2)), as shown in green. Then, when you calculate the hypotenuse from this triangle, you'll find that it’s sqrt(2+sqrt(2)), which is what we were looking for. You can repeat the process from this triangle, to build another 45-45-90 triangle, as shown in blue, with a hypotenuse of sqrt(2+sqrt(2+sqrt(2))), which of course, is the next iteration.
I'm sorry. Apparently I posted the wrong link for the image.
Just in case, it's: http://i411.photobucket.com/albums/pp194/watari_pag/asdf.gif
I don't know if people still look at this thread occasionally, but perhaps so, and indeed the questions posed by the youngster who started it (from G.H. Hardy's "A Course of Pure Mathematics") piqued my interest, so I thought I'd continue on nonetheless.
The second topic brought up in Hardy's book concerns geometrical constructions that provide solutions to quadratic equations. The one thing I found odd about Hardy's description of the problem was the way he set forth the basic quadratic equation as being of the form . Why did he put the 2 there? Moreover, he tells us that the roots of this equation are determined by , whereas most of us remember this as . Honestly, it's easier if you simply take the basic quadratic equation as being of the form , and then, in the geometrical construction, take PP' = -4a/b and QQ' = -c/b
To grasp the full range of these constructions, I suggest taking a look at F. Klein's "Famous Problems of Elementary Geometry," pp. 32-41, which is free in Google Books:
Regarding these geometrical constructions and why they work, Hardy notes, "The proof is simple and we leave it as an exercise to the reader." I confess though, for me, only after seeing the proof in Klein's book did I realize that yes it is fairly straightforward.
At any rate, to give one simple example of such a construction for
The second topic brought up in Hardy's book concerns geometrical constructions that provide solutions to quadratic equations. The one thing I found odd about Hardy's description of the problem was the way he set forth the basic quadratic equation as being of the form . Why did he put the 2 there? Moreover, he tells us that the roots of this equation are determined by , whereas most of us remember this as . Honestly, it's easier if you simply take the basic quadratic equation as being of the form , and then, in the geometrical construction, take PP' = -4a/b and QQ' = -c/b
To grasp the full range of these constructions, I suggest taking a look at F. Klein's "Famous Problems of Elementary Geometry," pp. 32-41, which is free in Google Books:
Regarding these geometrical constructions and why they work, Hardy notes, "The proof is simple and we leave it as an exercise to the reader." I confess though, for me, only after seeing the proof in Klein's book did I realize that yes it is fairly straightforward.
At any rate, to give one simple example of such a construction for
Spoiler
Oh no, my initial construction of nested square roots of 2 was not correct. Although the green triangle is correct, you cannot go on duplicating the process with similar and larger triangles, because the hypotenuse will just keep getting bigger, i.e., it already exceeds 2 in the blue triangle, whereas the nested square roots of 2 are supposed to converge to 2.
In other words, it's a geometric progression, with larger and larger hypotenuses, which does not correspond to the convergence to 2 of
as it should.
A correct construction (I'm sure there are others), which should be obvious can be created with a straightedge and compass, is shown below.
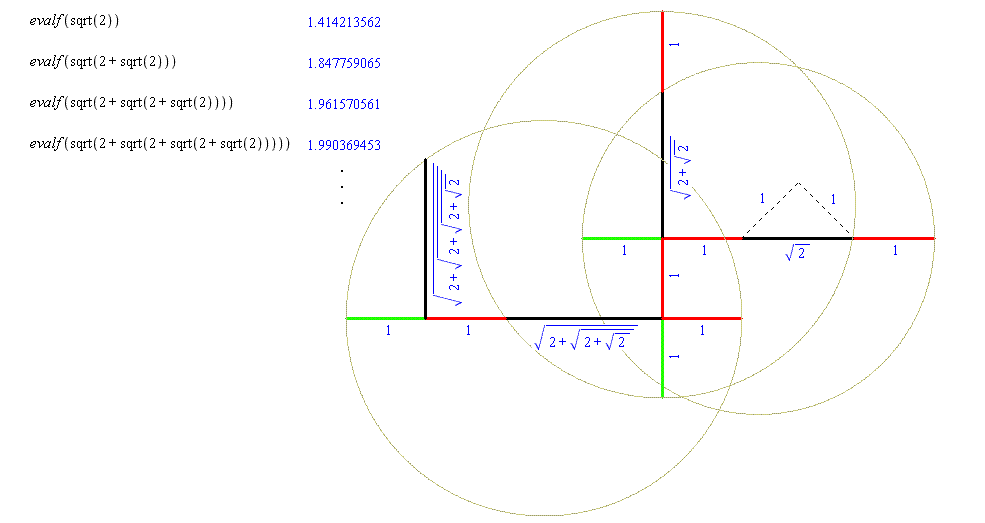
In other words, it's a geometric progression, with larger and larger hypotenuses, which does not correspond to the convergence to 2 of
as it should.
A correct construction (I'm sure there are others), which should be obvious can be created with a straightedge and compass, is shown below.

Quick Reply
Related discussions
- Teenagers find an "impossible" proof of Pythagoras' Theorem
- can anyone answer this A level vectors question (very challenging)
- Maths series help
- A level maths
- Help with complex summation further maths a levels
- Geometric Sum proof
- Arithmetic or geometric sequence
- A2 Sequence and Series
- Vaping in College Toilets
- Alevel maths - OCR
- A level maths sequences help
- Question on proof by induction for Inductive Sequences
- Exponentials question
- Relationship
- Sequence and series
- Arithmetic sequence diverge or converge formula?
- Negative Binomial Question
- I hate having big boobs
- Engineering.
- New Spec A Level Sequences
Latest
Trending
Last reply 2 days ago
Did Cambridge maths students find maths and further maths a level very easy?Last reply 2 weeks ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71
Trending
Last reply 2 days ago
Did Cambridge maths students find maths and further maths a level very easy?Last reply 2 weeks ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71





