C4 Integration question
Would appreciate some help with this question I'm finding tricky.
By using the substitution given, show that the LHS gives the RHS [6]
By using the substitution given, show that the LHS gives the RHS [6]
Original post by latslikeabat
Would appreciate some help with this question I'm finding tricky.
By using the substitution given, show that the LHS gives the RHS [6]
By using the substitution given, show that the LHS gives the RHS [6]
Whenever you post, explain what you have attempted to do or better, write that what you have done so far, where you have got to so then someone can better give you hints.
oops my bad.
well i got:

I then used the substition to form
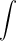
and hence
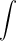
=
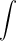
=
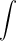
=
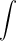
I wasn't sure what to do after this but considered using parts, however that seemed overly complex.
well i got:
I then used the substition to form
and hence
=
=
=
I wasn't sure what to do after this but considered using parts, however that seemed overly complex.
(edited 13 years ago)
Original post by latslikeabat
oops my bad.
well i got:

I then used the substition to form
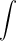
and hence
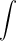
=
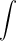
=
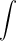
=
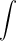
I wasn't sure what to do after this but considered using parts, however that seemed overly complex.
well i got:
I then used the substition to form
and hence
=
=
=
I wasn't sure what to do after this but considered using parts, however that seemed overly complex.
Ok great, can work with that. You've got the right idea but the notation is a bit sloppy though, in terms of what you're integrating with respect to. After the substitution, you want to be integrating with respect to theta, not a, a is just a constant here.
so
Changing limits and subbing in to put in terms of theta.
Original post by Clarity Incognito
Ok great, can work with that. You've got the right idea but the notation is a bit sloppy though, in terms of what you're integrating with respect to. After the substitution, you want to be integrating with respect to theta, not a, a is just a constant here.
so
Changing limits and subbing in to put in terms of theta.
so
Changing limits and subbing in to put in terms of theta.
Ah ok , that makes a lot more sense.
and so after that would you get:
and then use the double angle formula so that:
After that point would you use parts so that:
and
?
Also what is 'u' differentiated w.r.t?
Original post by latslikeabat
Ah ok , that makes a lot more sense.
and so after that would you get:
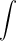
and then use the double angle formula so that:
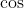
After that point would you use parts so that:
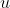
and
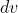
?
Also what is 'u' differentiated w.r.t?
and so after that would you get:
and then use the double angle formula so that:
After that point would you use parts so that:
and
?
Also what is 'u' differentiated w.r.t?
Since a is a constant you don't need to use "by parts". What do you get if you integrate 7 cos x? Just 7 sin x. Treat the a^2 like a 7.
Original post by latslikeabat
Ah ok , that makes a lot more sense.
Also what is 'u' differentiated w.r.t?
Also what is 'u' differentiated w.r.t?
a is just a constant so a^2 is also a constant. You can take it out of the integral. You're integrating with respect to theta.
Original post by irfan91
this is how you do it
Just a note, do you post full solutions, the point of the forum is to help users gain a better understanding, not to give them solutions. Please read the forum rules.
Original post by Clarity Incognito
a is just a constant so a^2 is also a constant. You can take it out of the integral. You're integrating with respect to theta.
Just a note, do you post full solutions, the point of the forum is to help users gain a better understanding, not to give them solutions. Please read the forum rules.
Just a note, do you post full solutions, the point of the forum is to help users gain a better understanding, not to give them solutions. Please read the forum rules.
lool sorry officer
Original post by irfan91
lool sorry officer
Haha, didn't mean for it to sound so angry, I just wanted to point it out, it's quite usual for members to let newer members know.

EDIT: Also, I just looked through your working and you don't account for the limits of substitution properly. The top limit should be pi/6 throughout and the bottom pi/2 unless you swap them and put a minus out front. The integral actually gives area under the x axis and as area is positive, you take the magnitude of the answer.
(edited 13 years ago)
Ok, now I get it.
Thanks for the help.
Thanks for the help.
Original post by Clarity Incognito
Haha, didn't mean for it to sound so angry, I just wanted to point it out, it's quite usual for members to let newer members know. 
EDIT: Also, I just looked through your working and you don't account for the limits of substitution properly. The top limit should be pi/6 throughout and the bottom pi/2 unless you swap them and put a minus out front. The integral actually gives area under the x axis and as area is positive, you take the magnitude of the answer.

EDIT: Also, I just looked through your working and you don't account for the limits of substitution properly. The top limit should be pi/6 throughout and the bottom pi/2 unless you swap them and put a minus out front. The integral actually gives area under the x axis and as area is positive, you take the magnitude of the answer.
its all good, yeah i tried it first time with the limits the other way round and i didn't get the RHS so i just flipped it to get the RHS, thanks for the advice and forum rules
Quick Reply
Related discussions
- Edexcel A2 Mathematics: Core Mathematics C4 6666 01 - 22 June 2018 [Exam Discussion]
- A-level maths help!
- A-Level Music Technology 2023
- integration
- Help urgent maths
- School behaviour record
- Volumes of revolution
- Integration
- A level maths mechanics question (1)
- Integration question
- Second Undergraduate Degree Funding
- polar coordinate question help
- Parametric integration
- Postgraduate Master's Loan - 2
- stuck on maths distribution question
- Integration
- what Integration technique should I be using?
- how tf do i start??? hyperbolics integration question
- Maths parametric integration
- Hard integration Q
Latest
Last reply 17 minutes ago
AQA A Level Sociology Paper 2 (7192/2) - 4th June 2024 [Exam Chat]Last reply 17 minutes ago
R u 18-25 & studying in a England Uni, spare a few mins to fill my survey. 1 wk left.Last reply 20 minutes ago
Edexcel A Level Economics A Paper 1 (9ECO 01) - 15th May 2024 [Exam Chat]Posted 27 minutes ago
st. andrews sixth form in cambridgeLast reply 45 minutes ago
Anyone else applying/has applied to UCL's Robotics and AI MEng course??Last reply 58 minutes ago
LSE International Social and Public Policy and Economics (LLK1) 2024 ThreadLast reply 1 hour ago
Official London School of Economics and Political Science 2024 Applicant ThreadLast reply 1 hour ago
Official University of the Arts London Applicant Thread for 2024Last reply 1 hour ago
LAWYERS: Can I bring an action against my old schoolLast reply 1 hour ago
JK Rowling in ‘arrest me’ challenge over hate crime lawLast reply 1 hour ago
Children to no longer be prescribed puberty blockers, NHS England confirmsTrending
Last reply 1 week ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71
Trending
Last reply 1 week ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71




