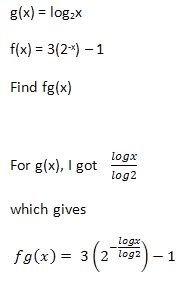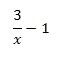Original post by buj
i can see the pattern emerging, but can anyone explain why this is? is it a rule or is there a way to come to this conclusion without a calculator?
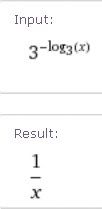
logn(x) and nx are inverse functions of each other, so they cancel.
First of all deal with the negative power. x^-a = 1 / x^a
So 2^(-log2(x)) = 1 / 2^(log2(x))
Taking logs is the opposite of raising something to a power so they sort of cancel out. If you think of base 10:
log10=1
so 10^(log10) = 10^1=10
log 100 = 2
so 10^(log100) = 10^2 = 100
Generally,
10^(log x) = x
This works for any base so 2^(log2(x)) = x
So 2^(-log2(x)) = 1/x
Putting this into f (x) should give the required result.
So 2^(-log2(x)) = 1 / 2^(log2(x))
Taking logs is the opposite of raising something to a power so they sort of cancel out. If you think of base 10:
log10=1
so 10^(log10) = 10^1=10
log 100 = 2
so 10^(log100) = 10^2 = 100
Generally,
10^(log x) = x
This works for any base so 2^(log2(x)) = x
So 2^(-log2(x)) = 1/x
Putting this into f (x) should give the required result.
Quick Reply
Related discussions
- -1^x = b is this solveable using natural logarithms?
- AS logs help
- In v=ab^t. What does b represent. Logb is the gradient I think but what is b. Thanks
- Edexcel A2 Mathematics: Core Mathematics C4 6666 01 - 22 June 2018 [Exam Discussion]
- A Level Maths : Common Mistakes/misconceptions
- C3
- A level OCR maths question help
- Topics that came up in the A2 Edexcel Maths Paper 1 2023?
- Excel - urgent help!!
- a level functions help pls !!
- Help urgent integration
- Oxbridge Maths - Interview Questions
- SPSS Assignment
- my student finance application isn't showing up when my parent tries to support it
- Range of a function
- a level math logs question
- Partial differentiation question
- York Offer Holder days (You@York)
- Money Revisited
- Composite functions
Latest
Last reply 50 minutes ago
Official University College London Applicant Thread for 2024Last reply 55 minutes ago
Can I do economics degree without a level maths?Last reply 1 hour ago
How to choose unis in UCAS application for CS undergraduate course?Last reply 1 hour ago
Rishi Sunak pledges to remove benefits for people not taking jobs after 12 monthsLast reply 2 hours ago
Got my crush's number 2 days ago and no reply yet. What could be the reasons?Posted 2 hours ago
GB News set to axe 40 jobs after channel posts heavy lossesLast reply 2 hours ago
Rwanda bill likely to be stalled at least till April after seven defeats in the LordsPosted 2 hours ago
Sunak rejects offer of youth mobility scheme between EU and UKTrending
Last reply 1 week ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71
Trending
Last reply 1 week ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71