Scroll to see replies

CIE and its Pure Maths 3
dunno I left all this **** behind when I graduated.
on your own kiddo
simplify
( cos 2θ + i(sin 2θ) - 1) ÷ ( cos 2θ + i(sin 2θ) + 1 )
show that it is equal to = i tanθ
I did it by converting into polar form and rationalising the denominator. How far have you gotten?
No. A different kind of rationalising and you made a mistake.

No. A different kind of rationalising and you made a mistake.

Can you type up your last line?
I don't get that. What did you multiply by to rationalise the denominator?
She hasn't multiplied anything, simply converted double angles into single angles for some obscure reason.
i used the double angle formula :
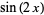
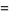
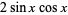 (1)
(1)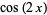
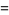
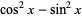 (2)
(2)
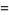
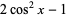 (3)
(3)
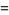
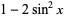
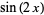
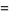
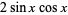 (1)
(1)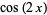
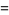
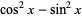 (2)
(2)
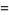
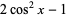 (3)
(3)
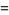
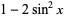
The + sign bolded above should be a - sign.
Rationalise the denominator, then use double angle fomulae if necessary. Otherwise it will get overcomplicated.
simplify
( cos 2θ + i(sin 2θ) - 1) ÷ ( cos 2θ + i(sin 2θ) + 1 )
show that it is equal to = i tanθ
There are probably more effective solutions but here is mine (refer to it only once you're done):
Spoiler
Multiply the fraction by (which is 1, obviously), you end up with terms of form which you can easily rewrite in terms of sin and cos theta.
You posted that one minute after I posted my method... Now I feel silly for complicating it.
Spoiler
Thanks! I used the same method as yours, and was stuck at simplifying it.. (sorry i actually took a peek before i'm actually done
 )
)Multiply the fraction by (which is 1, obviously), you end up with terms of form which you can easily rewrite in terms of sin and cos theta.
I tried your method, right after I finished the first try. And it really saves all the troubles! thank you.

Quick Reply
Related discussions
- A Level furthermaths
- Engineering complex numbers + trig help
- Complex numbers A level question
- I’m so confused about part B Argand diagrams
- Integral Maths - Complex numbers - Test C1
- How to find the complex numbers w in w^2-1=20(1-i)? please show the working out
- Roots of Equations Further Maths Help
- Archer's Road University of Southampton
- a level math
- AQA A Level Chemistry Transition metals
- What does 3<180 mean in the polynomial calculator mode?
- inequality involving modulus
- Self-teaching A-Level Further Mathematics in One Month Blog
- AS further maths - edexcel
- An inequation
- Question regarding personal statement - Maths
- Briggate studios - Leeds Beckett
- Complex argument
- Calculator not giving exact answers
- -1^x = b is this solveable using natural logarithms?
Latest
Trending
Last reply 1 day ago
Edexcel A Level Mathematics Paper 1 (9MA0 01) - 4th June 2024 [Exam Chat]Last reply 6 days ago
Edexcel IGCSE Higher tier Mathematics A Paper 1 1H (4MA1) - 8th November 2023Last reply 1 month ago
Edexcel GCSE Mathematics Paper 3 (1MA1 3) - 13th November 2023 [Exam Chat]Last reply 1 month ago
Edexcel GCSE Statistics Paper 1 Higher Tier (1ST0 1H) - 12th June 2023 [Exam Chat]284
Last reply 1 month ago
Edexcel A Level Mathematics Paper 1 (9MA0 01) - 6th June 2023 [Exam Chat]2960
Last reply 1 month ago
AQA A Level Mathematics Paper 1 (7357/1) - 6th June 2023 [Exam Chat]352
Last reply 2 months ago
Edexcel GCSE Mathematics Paper 2 (1MA1 2) - 10th November 2023 [Exam Chat]Last reply 2 months ago
Edexcel A-level Mathematics Paper 1 [6th June 2023] Unofficial Markscheme156
Last reply 2 months ago
Edexcel GCSE Mathematics Paper 1 (1MA1 1) - 8th November 2023 [Exam Chat]Last reply 3 months ago
Edexcel IGCSE Higher tier Mathematics A Paper 1 1H (4MA1) - 19th May 2023 [Exam Chat]232
Last reply 3 months ago
AQA GCSE Mathematics Paper 3 (Higher) 8300/3H - 14th June 2023 [ Exam Chat]247
Last reply 5 months ago
Edexcel IGCSE Higher tier Mathematics A Paper 2 2H (4MA1) - 10th November 2023Last reply 8 months ago
OCR A-level Mathematics A Paper 3 (H240/03) - 20th June 2023 [Exam Chat]169
Last reply 8 months ago
AQA Level 2 Further Maths 2023 Paper 1 (8365/1) & Paper 2 (8365/2) [Exam Chat]489
Last reply 8 months ago
Edexcel A Level Mathematics Paper 3 (9MA0 03) - 20th June 2023 [Exam Chat]1836
Last reply 8 months ago
AQA A Level Mathematics Paper 3 (7357/3) - 20th June 2023 [Exam Chat]307
Last reply 8 months ago
OCR A-level Mathematics B Paper 3 (H640/03) - 20th June 2023 [Exam Chat]132
Last reply 9 months ago
Edexcel A-level Further Mathematics Paper 1 (9FM0 01) - 25th May 2023 [Exam Chat]902
Trending
Last reply 1 day ago
Edexcel A Level Mathematics Paper 1 (9MA0 01) - 4th June 2024 [Exam Chat]Last reply 6 days ago
Edexcel IGCSE Higher tier Mathematics A Paper 1 1H (4MA1) - 8th November 2023Last reply 1 month ago
Edexcel GCSE Mathematics Paper 3 (1MA1 3) - 13th November 2023 [Exam Chat]Last reply 1 month ago
Edexcel GCSE Statistics Paper 1 Higher Tier (1ST0 1H) - 12th June 2023 [Exam Chat]284
Last reply 1 month ago
Edexcel A Level Mathematics Paper 1 (9MA0 01) - 6th June 2023 [Exam Chat]2960
Last reply 1 month ago
AQA A Level Mathematics Paper 1 (7357/1) - 6th June 2023 [Exam Chat]352
Last reply 2 months ago
Edexcel GCSE Mathematics Paper 2 (1MA1 2) - 10th November 2023 [Exam Chat]Last reply 2 months ago
Edexcel A-level Mathematics Paper 1 [6th June 2023] Unofficial Markscheme156
Last reply 2 months ago
Edexcel GCSE Mathematics Paper 1 (1MA1 1) - 8th November 2023 [Exam Chat]Last reply 3 months ago
Edexcel IGCSE Higher tier Mathematics A Paper 1 1H (4MA1) - 19th May 2023 [Exam Chat]232
Last reply 3 months ago
AQA GCSE Mathematics Paper 3 (Higher) 8300/3H - 14th June 2023 [ Exam Chat]247
Last reply 5 months ago
Edexcel IGCSE Higher tier Mathematics A Paper 2 2H (4MA1) - 10th November 2023Last reply 8 months ago
OCR A-level Mathematics A Paper 3 (H240/03) - 20th June 2023 [Exam Chat]169
Last reply 8 months ago
AQA Level 2 Further Maths 2023 Paper 1 (8365/1) & Paper 2 (8365/2) [Exam Chat]489
Last reply 8 months ago
Edexcel A Level Mathematics Paper 3 (9MA0 03) - 20th June 2023 [Exam Chat]1836
Last reply 8 months ago
AQA A Level Mathematics Paper 3 (7357/3) - 20th June 2023 [Exam Chat]307
Last reply 8 months ago
OCR A-level Mathematics B Paper 3 (H640/03) - 20th June 2023 [Exam Chat]132
Last reply 9 months ago
Edexcel A-level Further Mathematics Paper 1 (9FM0 01) - 25th May 2023 [Exam Chat]902



