Statistics S1
Hi,
I did this question from a past paper on the normal distribution and wasn't sure how to do it, and after looking at the mark scheme I still can't seem to understand how to do it, so was hoping someone can help.
A health club lets members use, on each visit, its facilities for as long as they wish. The club's records suggest that the length of a visit can be modelled by a normal distribtion with mean 90 minutes and standard deviation 41.587. Then club introduce a closing time of 10.00pm.
Tara arrives at the club at 8.00pm Explain whether or not this distribution is still a suitable model for the length of her visit.
The mark scheme states 90 + 3σ= 215 => 6.25 pm for latest arrival 90 + 2σ = 173.3 => 7.07 pm for latest arrival
Therefore this normal distribution is not suitable. (Based on 2σ/3σ rule)
Can someone please explain to me how what the mark scheme shows means that the distribution is not suitable, as I can't figure it out. Also, what is the '2σ/3σ rule'? Thank you very much for your help!
I did this question from a past paper on the normal distribution and wasn't sure how to do it, and after looking at the mark scheme I still can't seem to understand how to do it, so was hoping someone can help.
A health club lets members use, on each visit, its facilities for as long as they wish. The club's records suggest that the length of a visit can be modelled by a normal distribtion with mean 90 minutes and standard deviation 41.587. Then club introduce a closing time of 10.00pm.
Tara arrives at the club at 8.00pm Explain whether or not this distribution is still a suitable model for the length of her visit.
The mark scheme states 90 + 3σ= 215 => 6.25 pm for latest arrival 90 + 2σ = 173.3 => 7.07 pm for latest arrival
Therefore this normal distribution is not suitable. (Based on 2σ/3σ rule)
Can someone please explain to me how what the mark scheme shows means that the distribution is not suitable, as I can't figure it out. Also, what is the '2σ/3σ rule'? Thank you very much for your help!
Original post by Jacob4
Hi,
I did this question from a past paper on the normal distribution and wasn't sure how to do it, and after looking at the mark scheme I still can't seem to understand how to do it, so was hoping someone can help.
A health club lets members use, on each visit, its facilities for as long as they wish. The club's records suggest that the length of a visit can be modelled by a normal distribtion with mean 90 minutes and standard deviation 41.587. Then club introduce a closing time of 10.00pm.
Tara arrives at the club at 8.00pm Explain whether or not this distribution is still a suitable model for the length of her visit.
The mark scheme states 90 + 3σ= 215 => 6.25 pm for latest arrival 90 + 2σ = 173.3 => 7.07 pm for latest arrival
Therefore this normal distribution is not suitable. (Based on 2σ/3σ rule)
Can someone please explain to me how what the mark scheme shows means that the distribution is not suitable, as I can't figure it out. Also, what is the '2σ/3σ rule'? Thank you very much for your help!
I did this question from a past paper on the normal distribution and wasn't sure how to do it, and after looking at the mark scheme I still can't seem to understand how to do it, so was hoping someone can help.
A health club lets members use, on each visit, its facilities for as long as they wish. The club's records suggest that the length of a visit can be modelled by a normal distribtion with mean 90 minutes and standard deviation 41.587. Then club introduce a closing time of 10.00pm.
Tara arrives at the club at 8.00pm Explain whether or not this distribution is still a suitable model for the length of her visit.
The mark scheme states 90 + 3σ= 215 => 6.25 pm for latest arrival 90 + 2σ = 173.3 => 7.07 pm for latest arrival
Therefore this normal distribution is not suitable. (Based on 2σ/3σ rule)
Can someone please explain to me how what the mark scheme shows means that the distribution is not suitable, as I can't figure it out. Also, what is the '2σ/3σ rule'? Thank you very much for your help!
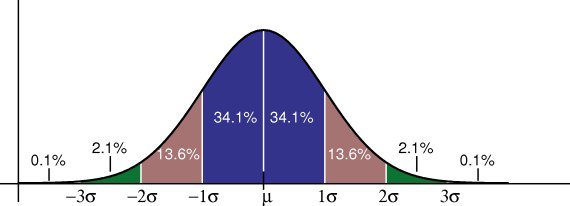
https://en.wikipedia.org/wiki/68%E2%80%9395%E2%80%9399.7_rule
These two things should help explain it for you

After you have read those things...
the question is using the rule to determine that:
from
90 + 2σ = 173, '95%' of visits will take less than 173 minutes. (This is not strictly true, it's actually 97.5% due to the other tail but doesn't matetr for what we're talking about)
And 215 is the '99.7%' where 99.7% (really 99.85, due to the tail) will take less than 215 minutes.
Hence for you to be 95% sure that no one will be there after 10pm, the latest visit start time should be the one given.
To be 99.7% sure, the earlier time of 6:25 is what is needed.
Hence if you put in 8pm then sometimes people's visits will go past 10pm which is not possible...and so..
Quick Reply
Related discussions
- Decision Maths or Statistics
- Confused in choosing the right combination for A2 in maths
- What units do I need for Edexcel IAL or IAS Further Maths
- CAIE S1 probability and P&C resources for intuitive understanding
- Messed up CIE Math P3 and Physics P4.
- 2nd Alevel RETAKE ...
- A levels for LSE accounting and finance
- A level math module
- A - levels for LSE
- How to have my school allow year 12 to choose a math subject for year 13.
- Geometric Sum proof
- Results Plus Direct Exam missing
- How bad are these Cambridge NSAA scores?
- Circuits Question
- BMAT percentage? Im at around 5.0,6.0,3A?
- Capacitor Question (PHYS)
- Maths as Edexcel kinematics help pls
- Official: Oxford A100 2024 Entry Applicants
- S1 and S2 Crib sheets (Edexcel)
- Parking on Campus at Sheffield Hallam
Latest
Last reply 2 minutes ago
Official Cambridge Postgraduate Applicants 2024 ThreadLast reply 4 minutes ago
AQA A Level Geography Paper 1 (7037/1) - 16th May 2024 [Exam Chat]Last reply 7 minutes ago
UAL art foundation 2024 diagnostic vs specialistLast reply 8 minutes ago
ATAS (Academic, Technology, Approval Scheme) Certificate 2023/2024Last reply 9 minutes ago
MPhil Advanced Computer Science Cambridge - 2024 EntryLast reply 9 minutes ago
Official Durham University Offer Holders Thread for 2024 entryLast reply 11 minutes ago
Offers for King’s College London (Portsmouth Branch) Graduate entry medicine A103Last reply 12 minutes ago
Edexcel A Level History Paper 1 (9HI0 1A-1H) - 23rd May 2024 [Exam Chat]Last reply 13 minutes ago
Accenture Degree Apprenticeship 2024



