C4 integration question
Attachment not found
I know that I wasn't supposed to use the limits 1/2 and 0 but I don't get how pi/6 is worked out. Thanks
Original post by coconut64
...
LImits for are 0 and . So with the substitution , you substitute in the limits of the integral and solve for to obtain the new limits.
Similarly, when x=0, theta = 0.
(edited 7 years ago)
Original post by coconut64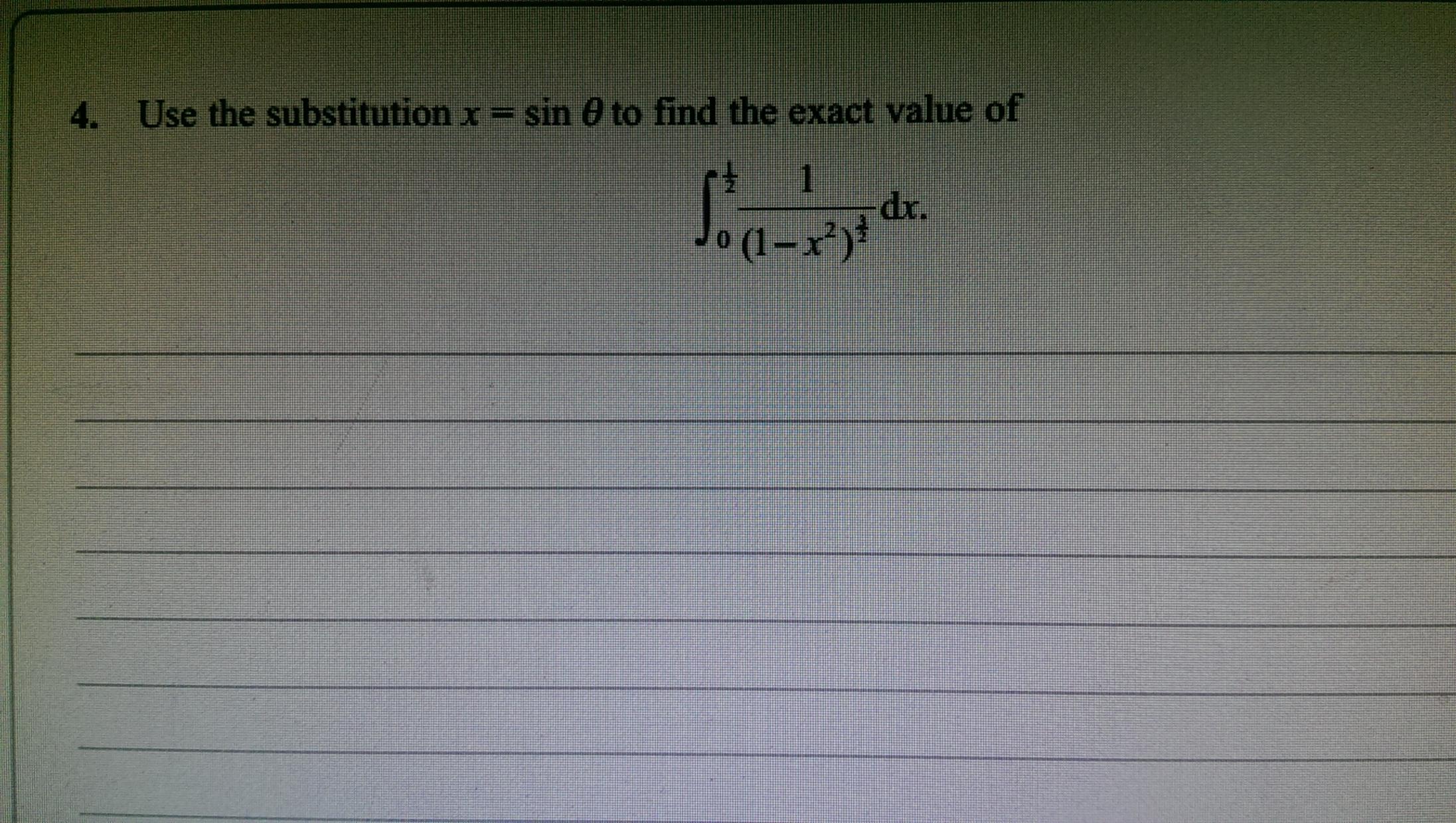 for this question I don't get his the limits are worked out.
for this question I don't get his the limits are worked out.
Thanks
Attachment not found
I know that I wasn't supposed to use the limits 1/2 and 0 but I don't get how pi/6 is worked out. Thanks
Once you make the substition you should either change the limits, as explained above, or write x = 0 and x = 1/2 on the integral.
Then after integrating either substitute back or change limits then, You must not 'mix up'and integration of u and x.
What you have written is incorrect ...
Original post by Muttley79
Once you make the substition you should either change the limits, as explained above, or write x = 0 and x = 1/2 on the integral.
Then after integrating either substitute back or change limits then, You must not 'mix up'and integration of u and x.
What you have written is incorrect ...
Then after integrating either substitute back or change limits then, You must not 'mix up'and integration of u and x.
What you have written is incorrect ...
I don't get what you mean by the bit underlined. Initially I subbed sin theta straight into the equation , rather than integrating the equation involving x. I did replace dx with d theta. I know where I have gone wrong with the limits..
Thanks
Original post by coconut64
I don't get what you mean by the bit underlined. Initially I subbed sin theta straight into the equation , rather than integrating the equation involving x. I did replace dx with d theta. I know where I have gone wrong with the limits..
Thanks
Thanks
Meaning you can ignore the limits until after you integrate. At which point, you may choose to convert your expression into terms of and apply the same limits, or instead you can change the limits to work with the expression in terms of
So at the stage of you could've either converted into (which doesn't really apply to this question well) OR but not a mix as you have there.
By I denote
(edited 7 years ago)
Original post by RDKGames
Meaning you can ignore the limits until after you integrate. At which point, you may choose to convert your expression into terms of and apply the same limits, or instead you can change the limits to work with the expression in terms of
So at the stage of you could've either converted into (which doesn't really apply to this question) OR but not a mix as you have there.
By I denote
So at the stage of you could've either converted into (which doesn't really apply to this question) OR but not a mix as you have there.
By I denote
So I just basically need to change the limit? Since I have already have my f(x) in place, which is tan theta. So are you suggesting that this should have been [tan theta] pi/6 on top and 0 at the bottom? Thanks
Original post by coconut64
So I just basically need to change the limit? Since I have already have my f(x) in place, which is tan theta. So are you suggesting that this should have been [tan theta] pi/6 on top and 0 at the bottom? Thanks
That is not , that is .
And yes that is what everyone on this thread is suggesting - the change in limits.
Original post by RDKGames
That is not , that is .
And yes that is what everyone on this thread is suggesting - the change in limits.
And yes that is what everyone on this thread is suggesting - the change in limits.
What is f(x)? X has been replaced by sin theta already, I don't understand what you mean by suddenly change it from f theta back to f(x), The equation has been simplified to sec^2 x.... If I do tan(pi/6) - tan(0), this gives me the answer which is 1/3 (root 3)
(edited 7 years ago)
Original post by coconut64
What is f(x)? X has been replaced by sin theta already, I don't understand what you mean by suddenly change it from f theta back to f(x), The equation has been simplified to sec^2 x....
With your particular question, is just in terms of (or ) which would be for some and replacing this in your integrated expression is too messy.
I'll give you a simple example concerning the two approaches.
then
So we have
Now we can either convert it back to and use the original limits in which case we have (this approach is not recommended for your Q) OR we can convert the limits so we have . Both of which give us the same answer.
(edited 7 years ago)
Original post by RDKGames
With your particular question, is just in terms of (or ) which would be for some and replacing this in your integrated expression is too messy.
I'll give you a simple example concerning the two approaches.
then
So we have
Now we can either convert it back to and use the original limits in which case we have (this approach is not recommended for your Q) OR we can convert the limits so we have . Both of which give us the same answer.
I'll give you a simple example concerning the two approaches.
then
So we have
Now we can either convert it back to and use the original limits in which case we have (this approach is not recommended for your Q) OR we can convert the limits so we have . Both of which give us the same answer.
To simplify this, are you suggesting my method takes too long?
Original post by coconut64
To simplify this, are you suggesting my method takes too long?
No, I'm only explaining what Muttley has stated when he said "You must not 'mix up'and integration of u and x" because that's what you've done with your method.
Original post by RDKGames
No, I'm only explaining what Muttley has stated when he said "You must not 'mix up'and integration of u and x" because that's what you've done with your method.
Sorry to drag on to this forever but I am more confused than ever.
Mutterfly said I shouldn't have mixed up u and x when integrating. I get where he is coming from, because I did not change the limits 0.5 &0, although I am integrating with respect with d theta. I understand this bit.
But you are suggesting that tan theta is equivalent to the orginal equation we are given x/ (1-x^2)^1.5 , but tan theta is obtained after I have integrated sec^2 x. Surely sec^2x is equal to sin theta / (1- x^2)^1.5. Thanks
Attachment not found
thanks(edited 7 years ago)
Original post by coconut64
Sorry to drag to this forever but I am more confused than ever.
Mutterfly said I shouldn't have mixed up u and x when integrating. I get where he is coming from, because I did not change the limits 0.5 &0, although I am integrating with respect with d theta. I understand this bit.
But you are suggesting that tan theta is equivalent to the orginal equation we are given x/ (1-x^2)^1.5 , but tan theta is obtained after I have integrated sec^2 x. Surely sec^2x is equal to sin theta / (1- x^2)^1.5. Thanks
Mutterfly said I shouldn't have mixed up u and x when integrating. I get where he is coming from, because I did not change the limits 0.5 &0, although I am integrating with respect with d theta. I understand this bit.
But you are suggesting that tan theta is equivalent to the orginal equation we are given x/ (1-x^2)^1.5 , but tan theta is obtained after I have integrated sec^2 x. Surely sec^2x is equal to sin theta / (1- x^2)^1.5. Thanks
I am not claiming it is equal to the original. The original is whereas I claim that for some - but this isn't a true enough statement as it's not true for all hence why this approach doesn't work very well. I have used a simpler integral to simply display the two approaches - which you now seem to understand.
(edited 7 years ago)
Original post by RDKGames
I am not claiming it is equal to the original. The original is whereas I claim that for some - but this isn't a true enough statement as it's not true for all hence why this approach doesn't work very well. I have used a simpler integral to simply display the two approaches - which you now seem to understand.
Since you can
Since you can
I have edited my post. Are you sure? The original equation is to the power of 1.5, not 1/2. Thanks
Original post by coconut64
I have edited my post. Are you sure? The original equation is to the power of 1.5, not 1/2. Thanks
Either way, yes I am sure because in either case I did not state that is equal to it as you claim.
Original post by RDKGames
Either way, yes I am sure because in either case I did not state that \tan(\theta) is equal to it as you claim.
I have checked, the original equation is to the power of 1.5, not 0.5. But I appreciate your help though.

Original post by coconut64
I have checked, the original equation is to the power of 1.5, not 0.5. But I appreciate your help though. 

(*) AFAIK, literally the only thing he's said about the original equation is "The original is ". Yes this isn't correct, but since he only quoted it to say "I'm not talking about the original integral I'm talking about " it doesn't invalidate anything else he said. He's still not talking about the original equation, and it still is a different equation from
Original post by coconut64
I have checked, the original equation is to the power of 1.5, not 0.5. But I appreciate your help though. 

Just to clarify further, you have defined
If you wish to keep your limits the same, then you must express in terms of thus express it in terms of . But you cannot define in terms of for all . You can sure try, and it works, but it doesn't hold for all theta hence why it breaks down when you come to use it and why the approach of simply changing the limits is the better option. To do this you would have to go
I have indicated the step where it breaks down by '=='
As said by DFranklin above, it has nothing to do with the original expression.
(edited 7 years ago)
Quick Reply
Related discussions
- Edexcel A2 Mathematics: Core Mathematics C4 6666 01 - 22 June 2018 [Exam Discussion]
- A-level maths help!
- A-Level Music Technology 2023
- integration
- Help urgent maths
- School behaviour record
- Volumes of revolution
- Integration
- A level maths mechanics question (1)
- polar coordinate question help
- Integration question
- Parametric integration
- Second Undergraduate Degree Funding
- Postgraduate Master's Loan - 2
- stuck on maths distribution question
- Integration
- what Integration technique should I be using?
- Maths parametric integration
- how tf do i start??? hyperbolics integration question
- Hard integration Q
Latest
Last reply 10 minutes ago
JK Rowling in ‘arrest me’ challenge over hate crime lawLast reply 10 minutes ago
Official University of Edinburgh Applicant Thread for 2024Trending
Last reply 1 week ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71
Trending
Last reply 1 week ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71



