C4 integration - two "right" answers??
Okay, well actually there is only one but HEAR ME OUT plz.
So I was trying to solve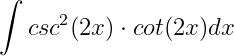
I did the idea of integrating a first order differential to get me back to the original function (+C!!!!!)
So I did y=-1/4 * csc^2(2x)
which when I put into WA, is identical to the integrand - But it's not the answer.
Why?!
So I was trying to solve
I did the idea of integrating a first order differential to get me back to the original function (+C!!!!!)
So I did y=-1/4 * csc^2(2x)
which when I put into WA, is identical to the integrand - But it's not the answer.
Why?!
Original post by DrSebWilkes
Okay, well actually there is only one but HEAR ME OUT plz.
So I was trying to solve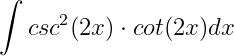
I did the idea of integrating a first order differential to get me back to the original function (+C!!!!!)
So I did y=-1/4 * csc^2(2x)
which when I put into WA, is identical to the integrand - But it's not the answer.
Why?!
So I was trying to solve
I did the idea of integrating a first order differential to get me back to the original function (+C!!!!!)
So I did y=-1/4 * csc^2(2x)
which when I put into WA, is identical to the integrand - But it's not the answer.
Why?!
I haven't checked this, but I'll assume you have everything right so far. When you say this isn't the answer, do you mean it is not the given answer? As in the mark schme or text book answer? Because if the differential of your answer is the original integrand, then it is correct. I expect that you will need to do some trig identity work to verify that your answer and their answer are, in fact, the same.
Original post by DrSebWilkes
Okay, well actually there is only one but HEAR ME OUT plz.
So I was trying to solve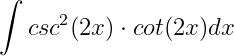
I did the idea of integrating a first order differential to get me back to the original function (+C!!!!!)
So I did y=-1/4 * csc^2(2x)
which when I put into WA, is identical to the integrand - But it's not the answer.
Why?!
So I was trying to solve
I did the idea of integrating a first order differential to get me back to the original function (+C!!!!!)
So I did y=-1/4 * csc^2(2x)
which when I put into WA, is identical to the integrand - But it's not the answer.
Why?!
Original post by Pangol
I haven't checked this, but I'll assume you have everything right so far. When you say this isn't the answer, do you mean it is not the given answer? As in the mark schme or text book answer? Because if the differential of your answer is the original integrand, then it is correct. I expect that you will need to do some trig identity work to verify that your answer and their answer are, in fact, the same.
Yeah as I said I went on WA and differentiated my "answer" and got exactly the integrand so I thought "brilliant" and left it.
I check the back and the answer is -1/4 cot^2(2x)
And WA says they are not equal (IE: not indentical) EDIT: ANNNND WA says the integral of the integrand is the back-of-book answer. Mystery deepens
Soooo ... yeah :| annoying this is I don't know many identities atm but I am trying to learn them. I'm trying to cram in C4 before November 2nd, you see
Original post by DFranklin
Note cosec^2 and cot^2 only differ by a constant, and you get an arbitrary constant when you integrate...
so, with a +C, am I right?
Original post by simon0
I presume where you mention "WA" you mean Wolfram Alpha.
Wolfram Alpha gives the antiderivative as (where C is a constant).
As DFranklin says, cot^{2} (x) and cosec^{2} (x) only differ by a constant.
Note, as under "Alternate forms of the integral", it lists:
Wolfram Alpha gives the antiderivative as (where C is a constant).
As DFranklin says, cot^{2} (x) and cosec^{2} (x) only differ by a constant.
Note, as under "Alternate forms of the integral", it lists:
As I mentioned, yeah.
But the point still remains that if you differentitate csc^2 (2x) * -1/4 you get the integrand.
So maybe that +C at the end takes care of it?
Original post by DrSebWilkes
As I mentioned, yeah.
But the point still remains that if you differentitate csc^2 (2x) * -1/4 you get the integrand.
So maybe that +C at the end takes care of it?
But the point still remains that if you differentitate csc^2 (2x) * -1/4 you get the integrand.
So maybe that +C at the end takes care of it?
Yes.
Quick Reply
Related discussions
- Edexcel A2 Mathematics: Core Mathematics C4 6666 01 - 22 June 2018 [Exam Discussion]
- St Andrews 5 year VS England 4 year degrees
- How do I get an A* in my History Coursework?
- GCSE Exam Discussions 2024
- gyg journal ⋆。‧˚ʚɞ˚‧。⋆
- OU plagiarism policy and application
- Giving more than one answer in an exam
- A-Level English Lit Revision Tips
- TMUA 2023 Thread
- Builder's nightmare -should i pay?
- Gcse English lit and lang
- Further mechanics successive oblique impacts
- AQA GCSE English Literature Paper 1 (8702/1) - 17th May [Exam Chat]
- A-Level English Literature ASND/Drama help please!
- Going from a C to A in english lit A-level
- English Literature
- Politics 25 mark extract question structure
- OCR A-Level English Literature
- Edexcel A Level English Literature Paper 1: Drama 9ET0 01 - 7 Jun 2022 [Exam Chat]
- OCR A Level English Lit... how do I get good?! (yr13)
Latest
Trending
Last reply 2 days ago
Did Cambridge maths students find maths and further maths a level very easy?Last reply 2 weeks ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71
Trending
Last reply 2 days ago
Did Cambridge maths students find maths and further maths a level very easy?Last reply 2 weeks ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71




