Capacitors
I was just wondering, if i had an ideal voltmeter across a capacitor with a resistor connected in series with it.
Then i had the same capacitor with the same resistor but instead i used an unideal voltmeter, how would the voltages with respect to time be different?
And also how would i create a circuit that could charge 2 capacitors separately and discharge them through the same resistor?
Would it look like this?
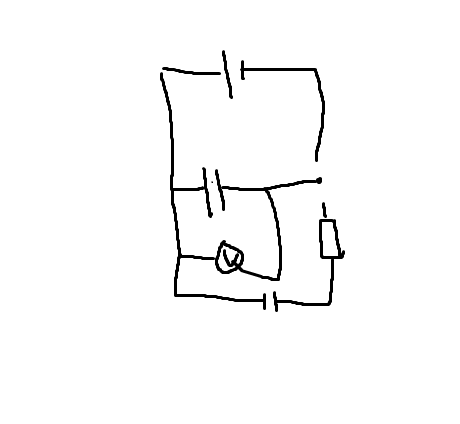
Then i had the same capacitor with the same resistor but instead i used an unideal voltmeter, how would the voltages with respect to time be different?
And also how would i create a circuit that could charge 2 capacitors separately and discharge them through the same resistor?
Would it look like this?
Scroll to see replies
Original post by Zenarthra
I was just wondering, if i had an ideal voltmeter across a capacitor with a resistor connected in series with it.
Then i had the same capacitor with the same resistor but instead i used an unideal voltmeter, how would the voltages with respect to time be different?
And also how would i create a circuit that could charge 2 capacitors separately and discharge them through the same resistor?
Would it look like this?

Then i had the same capacitor with the same resistor but instead i used an unideal voltmeter, how would the voltages with respect to time be different?
And also how would i create a circuit that could charge 2 capacitors separately and discharge them through the same resistor?
Would it look like this?
The circuit with the non-ideal voltmeter will have less resistance so I presume the change of voltage would be slower, since the energy can flow more freely in the circuit without being damped quite so much.
Consider the extreme case where the the voltmeter is so bad that it essentially has no resistance and the current just flows right through it. This would be a short circuit, meaning the current would take that path without giving much energy at all to the resistor, which would mean overall the voltage would remain high for longer.
The circuit you've drawn wouldn't work. It would charge the capacitors, but when you close the switch to let them discharge, the positive charge on the plates will have no way of flowing round to the other side.
Have you done simple harmonic motion yet? Capacitors can actually be considered as SHM systems. When you let them discharge, the charge oscillates from positive, around the circuit, to negative, and back again, continuously until the energy is dissipated. So as you can see in your circuit diagram, there is no way for the charge to oscillate from the positive plates around to the negative plates - it's all just stored on one side and then stays there.
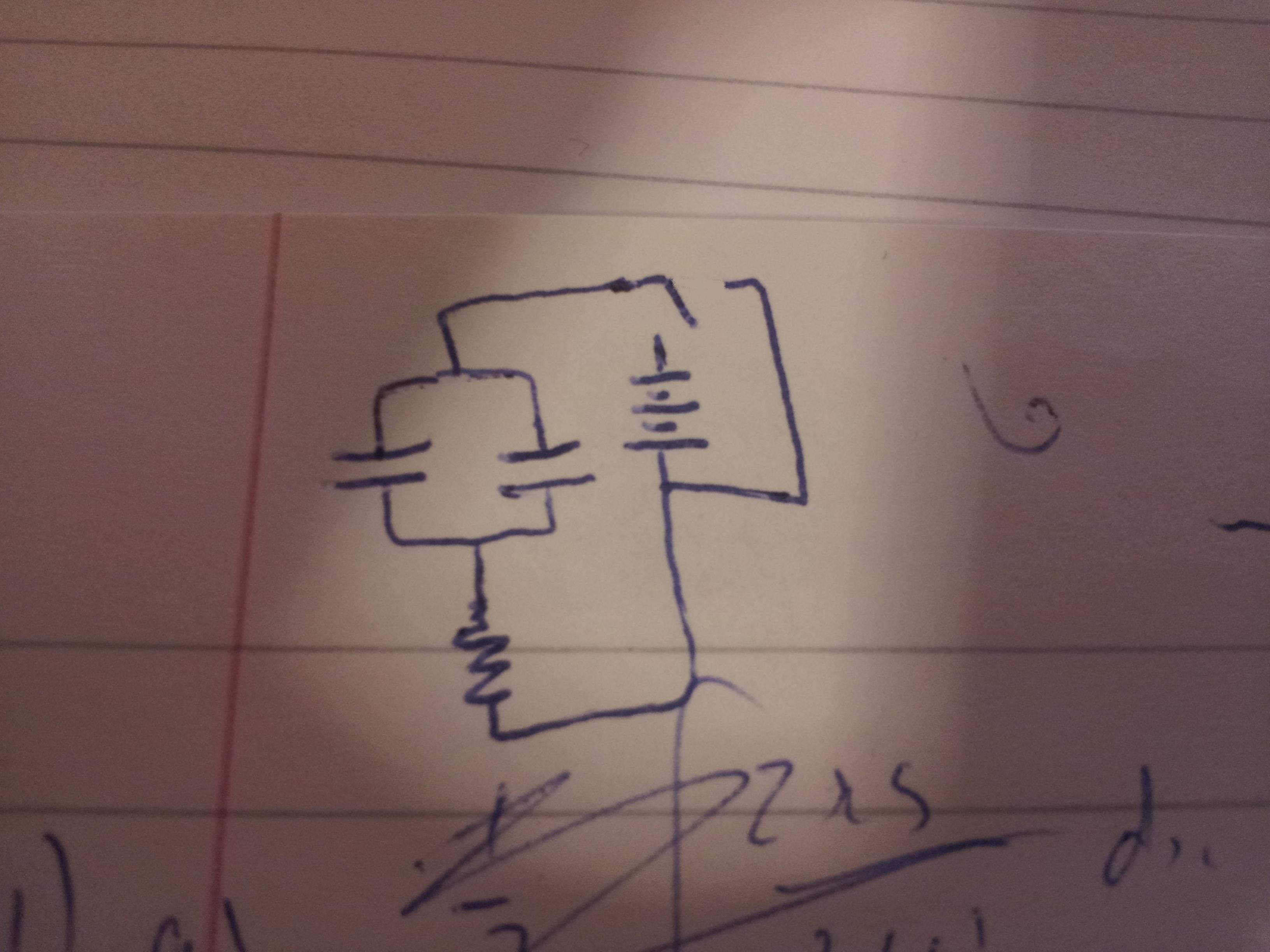
I've attached a circuit diagram that I think would work for what you wanted.
Original post by Pessimisterious
The circuit with the non-ideal voltmeter will have less resistance so I presume the change of voltage would be slower, since the energy can flow more freely in the circuit without being damped quite so much.
Consider the extreme case where the the voltmeter is so bad that it essentially has no resistance and the current just flows right through it. This would be a short circuit, meaning the current would take that path without giving much energy at all to the resistor, which would mean overall the voltage would remain high for longer.
The circuit you've drawn wouldn't work. It would charge the capacitors, but when you close the switch to let them discharge, the positive charge on the plates will have no way of flowing round to the other side.
Have you done simple harmonic motion yet? Capacitors can actually be considered as SHM systems. When you let them discharge, the charge oscillates from positive, around the circuit, to negative, and back again, continuously until the energy is dissipated. So as you can see in your circuit diagram, there is no way for the charge to oscillate from the positive plates around to the negative plates - it's all just stored on one side and then stays there.
I've attached a circuit diagram that I think would work for what you wanted.
Consider the extreme case where the the voltmeter is so bad that it essentially has no resistance and the current just flows right through it. This would be a short circuit, meaning the current would take that path without giving much energy at all to the resistor, which would mean overall the voltage would remain high for longer.
The circuit you've drawn wouldn't work. It would charge the capacitors, but when you close the switch to let them discharge, the positive charge on the plates will have no way of flowing round to the other side.
Have you done simple harmonic motion yet? Capacitors can actually be considered as SHM systems. When you let them discharge, the charge oscillates from positive, around the circuit, to negative, and back again, continuously until the energy is dissipated. So as you can see in your circuit diagram, there is no way for the charge to oscillate from the positive plates around to the negative plates - it's all just stored on one side and then stays there.
I've attached a circuit diagram that I think would work for what you wanted.
Hey thanks for the detail, is it possible to have an arrangment so that one capacitor discharges quicker than the other through the same resistor?
And if so how?
And yes i have done SHM,thanks for good explanation!
Thanks!
(edited 9 years ago)
Original post by Zenarthra
Hey thanks for the detail, is it possible to have an arrangment so that one capacitor discharges quicker than the other through the same resistor?
And if so how?
And yes i have done SHM,thanks for good explanation!
Thanks!
And if so how?
And yes i have done SHM,thanks for good explanation!
Thanks!
Cool, glad you were happy with it.
Hmmm, no I don't think it would be possible to have one discharging quicker than the other, at least not in the case of a simple circuit like we're dealing with here.
My reasoning behind this is based on kirchoff's current law. Even if one of the capacitors has a much greater capacity than the other, the currents from each capacitor still meet at a single junction when they go towards the resistor. If the flow of charge from one of the capacitors is much higher, it'll just push against the other capacitor and stop it from discharging, until they're both of equal charge and so can start to discharge together with equal current. Hence no capacitor will discharge faster than the other.
An interesting analogy would be that of when you hold a ruler flat at its edges on the palms of your hands. If you draw your hands slowly towards the middle, you'll notice that only one of your hands slides, until the friction balances and the other hand slides instead. Eventually you'll have moved your hands to the centre of the ruler and they will have both got there at the same time, regardless of whether you changed the speed of one hand or the other or whatever. The same thing happens for discharging capacitors if they both come in at the same junction to the same resistor. The one with the stronger current 'goes first', until it loses power and the other one gets to 'push in front'. It's a strange analogy but hopefully it makes sense!
Original post by Pessimisterious
Cool, glad you were happy with it.
Hmmm, no I don't think it would be possible to have one discharging quicker than the other, at least not in the case of a simple circuit like we're dealing with here.
My reasoning behind this is based on kirchoff's current law. Even if one of the capacitors has a much greater capacity than the other, the currents from each capacitor still meet at a single junction when they go towards the resistor. If the flow of charge from one of the capacitors is much higher, it'll just push against the other capacitor and stop it from discharging, until they're both of equal charge and so can start to discharge together with equal current. Hence no capacitor will discharge faster than the other.
An interesting analogy would be that of when you hold a ruler flat at its edges on the palms of your hands. If you draw your hands slowly towards the middle, you'll notice that only one of your hands slides, until the friction balances and the other hand slides instead. Eventually you'll have moved your hands to the centre of the ruler and they will have both got there at the same time, regardless of whether you changed the speed of one hand or the other or whatever. The same thing happens for discharging capacitors if they both come in at the same junction to the same resistor. The one with the stronger current 'goes first', until it loses power and the other one gets to 'push in front'. It's a strange analogy but hopefully it makes sense!
Hmmm, no I don't think it would be possible to have one discharging quicker than the other, at least not in the case of a simple circuit like we're dealing with here.
My reasoning behind this is based on kirchoff's current law. Even if one of the capacitors has a much greater capacity than the other, the currents from each capacitor still meet at a single junction when they go towards the resistor. If the flow of charge from one of the capacitors is much higher, it'll just push against the other capacitor and stop it from discharging, until they're both of equal charge and so can start to discharge together with equal current. Hence no capacitor will discharge faster than the other.
An interesting analogy would be that of when you hold a ruler flat at its edges on the palms of your hands. If you draw your hands slowly towards the middle, you'll notice that only one of your hands slides, until the friction balances and the other hand slides instead. Eventually you'll have moved your hands to the centre of the ruler and they will have both got there at the same time, regardless of whether you changed the speed of one hand or the other or whatever. The same thing happens for discharging capacitors if they both come in at the same junction to the same resistor. The one with the stronger current 'goes first', until it loses power and the other one gets to 'push in front'. It's a strange analogy but hopefully it makes sense!
Ahh ok.
I think 2 weeks ago we did an experiment with 2 capacitors, i forgot the arrangement but there was only 1 resistor and a voltmeter.
We charged the first capacitor to 3V and then measured the discharge time, it was quite quick.
Then we charged the other capacitor to 3V and discharged, this time it took longer for the voltage to drop.
Also it seemed to go down really slow something like this.
3V => 2.8 = > 2.7 => 2.6 => 2.5
Till it got to about 2V and it was hardly dropping.
Do you have any suggestions of what happened here?
Original post by Zenarthra
Ahh ok.
I think 2 weeks ago we did an experiment with 2 capacitors, i forgot the arrangement but there was only 1 resistor and a voltmeter.
We charged the first capacitor to 3V and then measured the discharge time, it was quite quick.
Then we charged the other capacitor to 3V and discharged, this time it took longer for the voltage to drop.
Also it seemed to go down really slow something like this.
3V => 2.8 = > 2.7 => 2.6 => 2.5
Till it got to about 2V and it was hardly dropping.
Do you have any suggestions of what happened here?
I think 2 weeks ago we did an experiment with 2 capacitors, i forgot the arrangement but there was only 1 resistor and a voltmeter.
We charged the first capacitor to 3V and then measured the discharge time, it was quite quick.
Then we charged the other capacitor to 3V and discharged, this time it took longer for the voltage to drop.
Also it seemed to go down really slow something like this.
3V => 2.8 = > 2.7 => 2.6 => 2.5
Till it got to about 2V and it was hardly dropping.
Do you have any suggestions of what happened here?
Yep, it's the exponential decay of the charge.
Probably you used one capacitor and discharged it, then maybe added the second capacitor in parallel, which would increase the overall capacitance so the voltage decays at a slower rate.
Have you learned the equation yet?
V=V0e-t/RC
By increasing the capacitance you have a larger 'C' so the voltage will decay less.
Original post by Pessimisterious
Yep, it's the exponential decay of the charge.
Probably you used one capacitor and discharged it, then maybe added the second capacitor in parallel, which would increase the overall capacitance so the voltage decays at a slower rate.
Have you learned the equation yet?
V=V0e-t/RC
By increasing the capacitance you have a larger 'C' so the voltage will decay less.
Probably you used one capacitor and discharged it, then maybe added the second capacitor in parallel, which would increase the overall capacitance so the voltage decays at a slower rate.
Have you learned the equation yet?
V=V0e-t/RC
By increasing the capacitance you have a larger 'C' so the voltage will decay less.
Ahh yes ofcourse.
Would the graphs for a non ideal voltmeter look something like this?
Would this be the correct explanation, consider the bottom diagram in the attached,
The current is split 3 times, for first capacitor for second capacitor and for voltmeter.
Total current through circuit is given by V=IR
Voltage across each component in parallel is same.
Since current is drawn away from the other capacitors then charging the capacitors would take longer as Q=It for the same amount of charge transfer t would have to be greater since I is less now across each capacitor.
And for Discharging V=V0e-t/RC
So if i record V=3 t=0, V=2.5 t=2, V=2 t=2
I know it wouldnt because of the exponential decay formula, but would the time just be greater eg. V=3 t=0, V=2.5 t=5, V=2 t=8
What would happen to these values and why?
Thanks!
Original post by Zenarthra
Ahh yes ofcourse.
Would the graphs for a non ideal voltmeter look something like this?
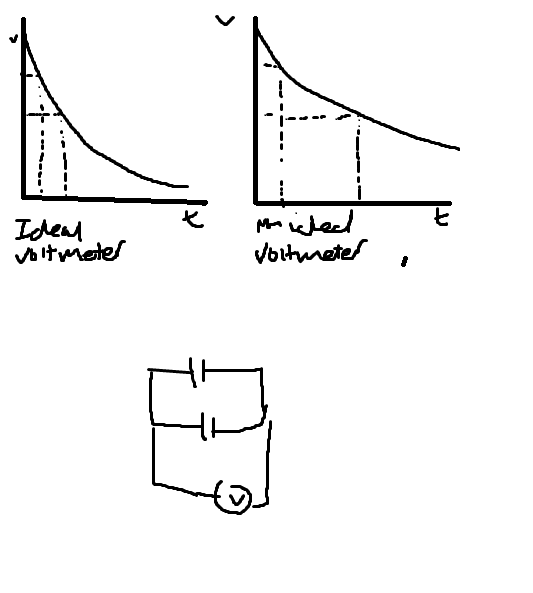
Would the graphs for a non ideal voltmeter look something like this?
An ideal voltmeter has infinite resistance since it should not draw any current from the circuit to be measured.
The CR time constant woud therefore also be infinite. i.e. all of the charge would remain on the capacitor and not discharge via the voltmeter.
The ideal V/t curve would be a flat line of magnitide Vc and t= infinity.
Original post by uberteknik
An ideal voltmeter has infinite resistance since it should not draw any current from the circuit to be measured.
The CR time constant woud therefore also be infinite. i.e. all of the charge would remain on the capacitor and not discharge via the voltmeter.
The ideal V/t curve would be a flat line of magnitide Vc and t= infinity.
The CR time constant woud therefore also be infinite. i.e. all of the charge would remain on the capacitor and not discharge via the voltmeter.
The ideal V/t curve would be a flat line of magnitide Vc and t= infinity.
Im sorry i dont understand.

I drew two graphs, 1 for a capacitor discharging through a resistor which has an ideal voltmeter across it.
And i then drew a graph for the same capacitor discharging through the same resistor which has a non ideal voltmeter across it.
How would the values of V shown on the voltmeter for discharging be different from the ideal voltmeter readings?
Perhaps i wasn't so clear, sorry.

Thanks!
Original post by Zenarthra
Im sorry i dont understand. 
I drew two graphs, 1 for a capacitor discharging through a resistor which has an ideal voltmeter across it.
And i then drew a graph for the same capacitor discharging through the same resistor which has a non ideal voltmeter across it.
How would the values of V shown on the voltmeter for discharging be different from the ideal voltmeter readings?
Perhaps i wasn't so clear, sorry.
Thanks!

I drew two graphs, 1 for a capacitor discharging through a resistor which has an ideal voltmeter across it.
And i then drew a graph for the same capacitor discharging through the same resistor which has a non ideal voltmeter across it.
How would the values of V shown on the voltmeter for discharging be different from the ideal voltmeter readings?
Perhaps i wasn't so clear, sorry.

Thanks!
Ahhh. That makes more sense.
So in the first case the ideal voltmeter follows the decaying voltage across the capacitor since the resistor is in parallel with the capacitor. (i.e. both the resistor and capacitor are connected at the same points and therefore the same voltage potential must exist across both. This is a bit confusing because at first glance a lot of people think the resistor is in series because of the current flow in the conductors.
Vcap = Vres = V0.(e-t/CR); time constant = CR
In the case where the voltmeter is non-ideal, it therefore has a finite resistance. Since this is also in parallel with the resistor, the combined resistance of the two is therefore:
Rparallel = (R x Rvm) / (R + Rvm)
Vcap = Vres = V0.(e-t/CRparallel), time constant = CRparallel
Since Rparlallel will always be less than R for a non-ideal voltmeter, the time constant will be smaller. Hence the capacitor wil discharge faster.
i.e. the exponential decay in the second graph (non-ideal voltmeter) will be steeper than for the ideal voltmeter.
(edited 9 years ago)
Original post by uberteknik
Ahhh. That makes more sense.
So in the first case the ideal voltmeter follows the decaying voltage across the capacitor since the resistor is in parallel with the capacitor. (i.e. both the resistor and capacitor are connected at the same points and therefore the same voltage potential must exist across both. This is a bit confusing because at first glance a lot of people think the resistor is in series because of the current flow in the conductors.
Vcap = Vres = V0.(e-t/CR); time constant = CR
In the case where the voltmeter is non-ideal, it therefore has a finite resistance. Since this is also in parallel with the resistor, the combined resistance of the two is therefore:
Rparallel = (R x Rvm) / (R + Rvm)
Vcap = Vres = V0.(e-t/CRparallel), time constant = CRparallel
Since Rparlallel will always be less than R for a non-ideal voltmeter, the time constant will be smaller. Hence the capacitor wil discharge faster.
i.e. the exponential decay in the second graph (non-ideal voltmeter) will be steeper than for the ideal voltmeter.
So in the first case the ideal voltmeter follows the decaying voltage across the capacitor since the resistor is in parallel with the capacitor. (i.e. both the resistor and capacitor are connected at the same points and therefore the same voltage potential must exist across both. This is a bit confusing because at first glance a lot of people think the resistor is in series because of the current flow in the conductors.
Vcap = Vres = V0.(e-t/CR); time constant = CR
In the case where the voltmeter is non-ideal, it therefore has a finite resistance. Since this is also in parallel with the resistor, the combined resistance of the two is therefore:
Rparallel = (R x Rvm) / (R + Rvm)
Vcap = Vres = V0.(e-t/CRparallel), time constant = CRparallel
Since Rparlallel will always be less than R for a non-ideal voltmeter, the time constant will be smaller. Hence the capacitor wil discharge faster.
i.e. the exponential decay in the second graph (non-ideal voltmeter) will be steeper than for the ideal voltmeter.
Ahh im talking about discharging through this kind of setup:
So the resistor is in parallel to the capacitors?
Original post by Zenarthra
Ahh im talking about discharging through this kind of setup:
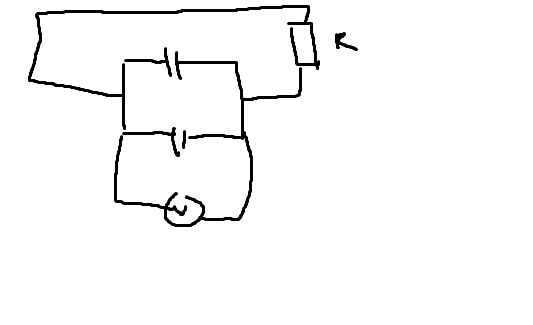
So the resistor is in parallel to the capacitors?
So the resistor is in parallel to the capacitors?
Yes.
All of the components in your diagram are in parallel.
Which is exactly as described in my last post.
Original post by uberteknik
Yes.
All of the components in your diagram are in parallel.
Which is exactly as described in my last post.
All of the components in your diagram are in parallel.
Which is exactly as described in my last post.
Oh, thank you so much!
I never knew it was in parallel to the others.
So the values of V would have a smaller t value?
And the graph would look something like this?
Original post by Zenarthra
Oh, thank you so much!
I never knew it was in parallel to the others.
So the values of V would have a smaller t value?
And the graph would look something like this?

I never knew it was in parallel to the others.
So the values of V would have a smaller t value?
And the graph would look something like this?

Original post by uberteknik
Exactly. 

2 more questions
Was this what i said correct?
The current is split 3 times, for first capacitor for second capacitor and for voltmeter.
Total current through circuit is given by V=IR
Voltage across each component in parallel is same.
Since current is drawn away from the other capacitors then charging the capacitors would take longer as Q=It for the same amount of charge transfer t would have to be greater since I is less now across each capacitor.
And also would a graph of Energy stored on a capacitor be 1 or 2 in this picture?
ThankS!
Original post by Zenarthra
2 more questions
Was this what i said correct?
The current is split 3 times, for first capacitor for second capacitor and for voltmeter.
Total current through circuit is given by V=IR
Voltage across each component in parallel is same.
Since current is drawn away from the other capacitors then charging the capacitors would take longer as Q=It for the same amount of charge transfer t would have to be greater since I is less now across each capacitor.
And also would a graph of Energy stored on a capacitor be 1 or 2 in this picture?
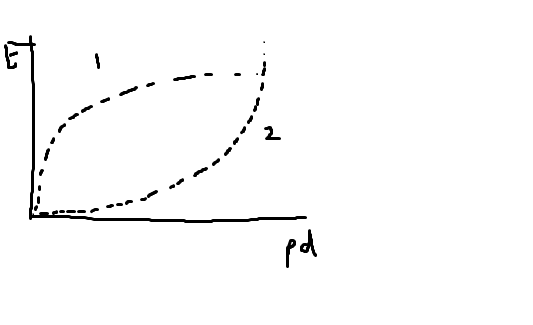
ThankS!
Was this what i said correct?
The current is split 3 times, for first capacitor for second capacitor and for voltmeter.
Total current through circuit is given by V=IR
Voltage across each component in parallel is same.
Since current is drawn away from the other capacitors then charging the capacitors would take longer as Q=It for the same amount of charge transfer t would have to be greater since I is less now across each capacitor.
And also would a graph of Energy stored on a capacitor be 1 or 2 in this picture?
ThankS!
Before we go any further, can you explain what you are trying to do first?
Total current I = V/R
pd across all parallel components is the same.
Energy stored = 1/2 CV2; the energy profile will therefore follow the same shape curve as the charge.
Original post by uberteknik
Before we go any further, can you explain what you are trying to do first?
Total current I = V/R
pd across all parallel components is the same.
Energy stored = 1/2 CV2; the energy profile will therefore follow the same shape curve as the charge.
Total current I = V/R
pd across all parallel components is the same.
Energy stored = 1/2 CV2; the energy profile will therefore follow the same shape curve as the charge.
So im trying to explain for a non ideal voltmeter across two capacitors in a parallel setup charging through a resistor also in parallel.
Im saying that since the voltmeter has finite resistance, it draws current away from the circuit.
The total resistance of the circuit is given by V=IR, I=V/R since V is constant and resistance of the whole circuit decreases, the current in the circuit must increase.
Current is split at the junction, between the two capacitors and the voltmeter.
What im not sure is if the charging time would increase or not, because there is an increase in current but also the current is split between 3 components now.
C=Q/V=It/V
Does the current through the two capacitors increase or decrease as we use a finite resistance voltmeter?
ThankS!
Original post by Zenarthra
So im trying to explain for a non ideal voltmeter across two capacitors in a parallel setup charging through a resistor also in parallel.
ThankS!
ThankS!
Woah! How does a capacitor charge through a parallel resistor?
I think you still have a few misconceptions but it's now very late. I will look at this again in the morning and we will try and help you sort them out.

Original post by uberteknik
Woah! How does a capacitor charge through a parallel resistor?
I think you still have a few misconceptions but it's now very late. I will look at this again in the morning and we will try and help you sort them out.
I think you still have a few misconceptions but it's now very late. I will look at this again in the morning and we will try and help you sort them out.

I was talking about charging through this resistor and i asked you if this resistor was in parallel to all the other and you said yes. O_O
Sorry, i think im confusing myself.

Original post by uberteknik
Woah! How does a capacitor charge through a parallel resistor?
I think you still have a few misconceptions but it's now very late. I will look at this again in the morning and we will try and help you sort them out.
I think you still have a few misconceptions but it's now very late. I will look at this again in the morning and we will try and help you sort them out.

Help please its important xD
Quick Reply
Related discussions
- OCR A Physics 2018 paper 2 capacitors
- Confusing Capacitor question
- Capacitor Question (PHYS)
- Hnc electrical engineering maths question
- A level physics capacitors
- A level physics question Capacitance (2)
- HNC electrical engineering maths question
- Hypothesis Testing
- need help please!
- Impedance
- Capacitors
- Capacitance
- Physics Question help
- hypothesis Testing with only > Mean side of z table
- Hard Capacitor Question AQA A Level Physics
- Unit 1 engineering design for hnc... Ideas
- Engineering maths help
- Physics OCR A-level PAG 9.2
- Direction of election flow in Capacitors
- Isaac physics A Square Pulse C3 - PLEASE help



