Original post by Sasuto
I am stuck on part b.
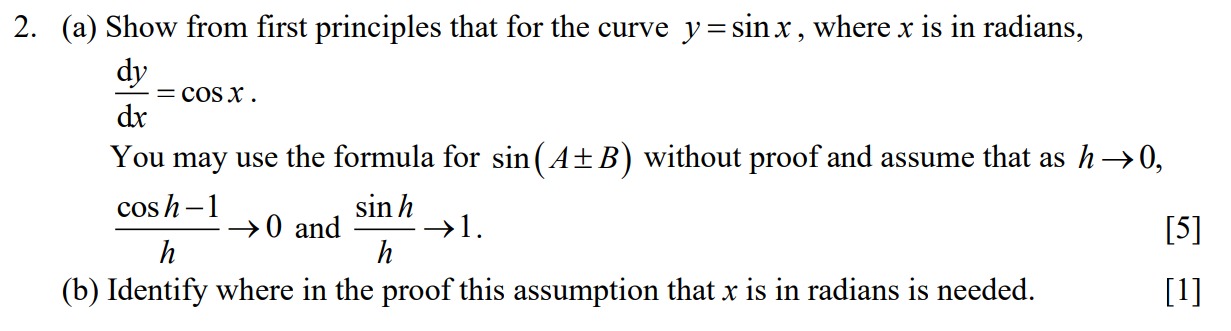
Here is my working:

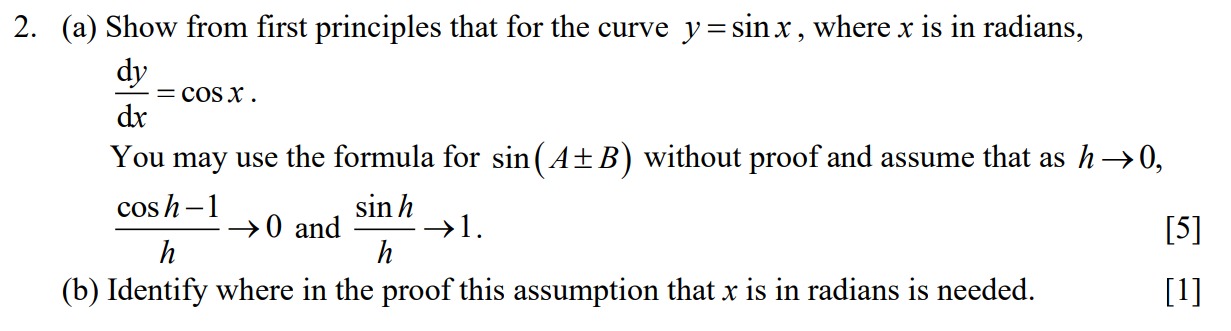
Here is my working:

If its in degrees, what is
sin(1) / 1
say? Here h=1 which is small in degrees, but pick any small value you want.
Original post by mqb2766
If its in degrees, what is
sin(1) / 1
say? Here h=1 which is small in degrees, but pick any small value you want.
sin(1) / 1
say? Here h=1 which is small in degrees, but pick any small value you want.
If it's in degrees sin(1)/1 is very close to zero so I think that negates the assumption that sin(h)/h=1. However if it's in radians, it's close to 1, making the assumption valid. Is this the right idea?
Original post by Sasuto
If it's in degrees sin(1)/1 is very close to zero so I think that negates the assumption that sin(h)/h=1. However if it's in radians, it's close to 1, making the assumption valid. Is this the right idea?
Sort of, but you must realise that the behaviour will be the same, irrespective of how you measure the angle (degrees or radians). So maybe work out how close it is to zero, compare it with what you get when h=2, 0.5, ... can you "guess" what the number corresponds to when thinking about degress and radians?
Original post by mqb2766
Sort of, but you must realise that the behaviour will be the same, irrespective of how you measure the angle (degrees or radians). So maybe work out how close it is to zero, compare it with what you get when h=2, 0.5, ... can you "guess" what the number corresponds to when thinking about degress and radians?
In degrees:
When h=1000 I get -0.0009848
When h=10 I get 0.01736...
When h=π I get 0.01744...
When h=0.1 I get 0.01745...
When h=0.01 I get 0.01745...
As h→0, value=π/180 ;and this is how you convert to radians, you multiply by π/180. Not sure if this is relevant...
As h→∞, value=0
In radians:
When h=10 I get -0.05440...
When h=π I get 0
When h=0.1 I get 0.9983...
When h=0.01 I get 0.99998...
As h→0, value=1 and I think this is the most relevant deduction.
As h→∞, value=0
This kinda relates to the small angle approximation idea, right? That sinx≈x.
So, relating back to the original question part c), the assumption that radians is needed should be identified where they say sin(h)/h→1 because for degrees, there's no general value of convergence, or it never equals 1. But in radians, it does when h→0. I seriously hope this is along the right lines.
Man, I feel like I am thinking too much for a 1 marker. But hey, what's maths without the rigour...?
Original post by Sasuto
In degrees:
When h=1000 I get -0.0009848
When h=10 I get 0.01736...
When h=π I get 0.01744...
When h=0.1 I get 0.01745...
When h=0.01 I get 0.01745...
As h→0, value=π/180 ;and this is how you convert to radians, you multiply by π/180. Not sure if this is relevant...
As h→∞, value=0
In radians:
When h=10 I get -0.05440...
When h=π I get 0
When h=0.1 I get 0.9983...
When h=0.01 I get 0.99998...
As h→0, value=1 and I think this is the most relevant deduction.
As h→∞, value=0
This kinda relates to the small angle approximation idea, right? That sinx≈x.
So, relating back to the original question part c), the assumption that radians is needed should be identified where they say sin(h)/h→1 because for degrees, there's no general value of convergence, or it never equals 1. But in radians, it does when h→0. I seriously hope this is along the right lines.
Man, I feel like I am thinking too much for a 1 marker. But hey, what's maths without the rigour...?
When h=1000 I get -0.0009848
When h=10 I get 0.01736...
When h=π I get 0.01744...
When h=0.1 I get 0.01745...
When h=0.01 I get 0.01745...
As h→0, value=π/180 ;and this is how you convert to radians, you multiply by π/180. Not sure if this is relevant...
As h→∞, value=0
In radians:
When h=10 I get -0.05440...
When h=π I get 0
When h=0.1 I get 0.9983...
When h=0.01 I get 0.99998...
As h→0, value=1 and I think this is the most relevant deduction.
As h→∞, value=0
This kinda relates to the small angle approximation idea, right? That sinx≈x.
So, relating back to the original question part c), the assumption that radians is needed should be identified where they say sin(h)/h→1 because for degrees, there's no general value of convergence, or it never equals 1. But in radians, it does when h→0. I seriously hope this is along the right lines.
Man, I feel like I am thinking too much for a 1 marker. But hey, what's maths without the rigour...?
Youre right, the understanding is not necessary for 1 mark and simply noting that sin(h)/h is not 1 would get you the mark.
For the understanding, you could note
pi/180 = 0.01745329251
and see if you can fill in the rest.
Original post by mqb2766
Youre right, the understanding is not necessary for 1 mark and simply noting that sin(h)/h is not 1 would get you the mark.
Well, that's much better. LOL
Sorry I'm not quite following, what do you mean by fill in the rest? The rest of the digits of pi/180?
Original post by Sasuto
Well, that's much better. LOL
Sorry I'm not quite following, what do you mean by fill in the rest? The rest of the digits of pi/180?
Sorry I'm not quite following, what do you mean by fill in the rest? The rest of the digits of pi/180?
Fill in the rest meant pi/180 is obviously the degrees -> radians multiplier so just understand why this is the limit value when things are measured in degrees.
Original post by mqb2766
Fill in the rest meant pi/180 is obviously the degrees -> radians multiplier so just understand why this is the limit value when things are measured in degrees.
Ah. Sorry, you can probably tell there's something happening to me. Why can I not read and understand the most basic thingsT^T
But thank you so much for putting up with my responses LOL
Enjoy your evening!
It seems I've already repped you previously. Kudos to you then!
(edited 9 months ago)
Original post by mqb2766
If its in degrees, what is
sin(1) / 1
say? Here h=1 which is small in degrees, but pick any small value you want.
sin(1) / 1
say? Here h=1 which is small in degrees, but pick any small value you want.
Arguably, "that's not my (your) problem". If the question says without qualification (*) that you may assume (sin h)/h -> 1, I'm not sure you can really say the proof relies on x being in radians.
Arguably I'm being pedantic, but I don't think it's actually unreasonable to assume you can "trust" things the question says you can assume.
Obviously what you're saying is what the examiner is after but I don't think it's a well worded question.
(*) I suppose the question does mention radians, but it doesn't state it's using radians in the sin h / h result. Again, it's bad wording IMHO.
(edited 9 months ago)
Original post by DFranklin
Arguably, "that's not my (your) problem". If the question says without qualification (*) that you may assume (sin h)/h -> 1, I'm not sure you can really say the proof relies on x being in radians.
Arguably I'm being pedantic, but I don't think it's actually unreasonable to assume you can "trust" things the question says you can assume.
Obviously what you're saying is what the examiner is after but I don't think it's a well worded question.
(*) I suppose the question does mention radians, but it doesn't state it's using radians in the sin h / h result. Again, it's bad wording IMHO.
Arguably I'm being pedantic, but I don't think it's actually unreasonable to assume you can "trust" things the question says you can assume.
Obviously what you're saying is what the examiner is after but I don't think it's a well worded question.
(*) I suppose the question does mention radians, but it doesn't state it's using radians in the sin h / h result. Again, it's bad wording IMHO.
Id guess the x on the first line is referring to an arbitrary variable. So both x and h in x+h would be in rads as in the usual interpretation?
Original post by mqb2766
Id guess the x on the first line is referring to an arbitrary variable. So both x and h in x+h would be in rads as in the usual interpretation?
My gut feeling looking at this question was the same as DFranklin's - the radians assumption is implicit in the limit result(s) they've given you, and isn't used elsewhere in the proof. My (facetious) answer to the question as stated would be "x needs to be in radians because the results on limits that you've quoted in the question rely on angles being in radians, you terminal ****** [insert abusive term as required]".
Not sure where this question come from, but it really does seem to be a badly worded attempt to test the student's understanding of something that isn't actually directly assumed in their [the student's] working

Original post by davros
My gut feeling looking at this question was the same as DFranklin's - the radians assumption is implicit in the limit result(s) they've given you, and isn't used elsewhere in the proof. My (facetious) answer to the question as stated would be "x needs to be in radians because the results on limits that you've quoted in the question rely on angles being in radians, you terminal ****** [insert abusive term as required]".
Not sure where this question come from, but it really does seem to be a badly worded attempt to test the student's understanding of something that isn't actually directly assumed in their [the student's] working
Not sure where this question come from, but it really does seem to be a badly worded attempt to test the student's understanding of something that isn't actually directly assumed in their [the student's] working

The double angle identity can be degrees/rads/... so the only part where the degrees/rad difference can give a difference is the limits as you say. Its a 1 marker, and Id guess people would "know" the stated limits were for rads, but Id be on the fence about whether its badly worded. No strong opinion either way.
@mqb2766, @davros - to go somewhat "meta" (and I've already taken us that way really) - I think what I don't like is that I think it's reasonable to put "you may assume' results in a "these are things I don't have to worry about" mental box. And then you're not even considering them when asked "why does this proof depend upon XYZ"?
In this case it's hopefully obvious enough no-one would be confused.
But you could imagine an analysis question with "you may assume the series on the right converges" and if the question asked at the end "why is this result only valid for small h" I think it would be very reasonable to not realise "because the series on the right would then diverge" was the expected answer - (particularly if it's not immediately obvious it would diverge).
Not the biggest deal in the world though.
In this case it's hopefully obvious enough no-one would be confused.
But you could imagine an analysis question with "you may assume the series on the right converges" and if the question asked at the end "why is this result only valid for small h" I think it would be very reasonable to not realise "because the series on the right would then diverge" was the expected answer - (particularly if it's not immediately obvious it would diverge).
Not the biggest deal in the world though.
(edited 9 months ago)
Original post by DFranklin
@mqb2766, @davros - to go somewhat "meta" (and I've already taken us that way really) - I think what I don't like is that I think it's reasonable to put "you may assume' results in a "these are things I don't have to worry about" mental box. And then you're not even considering them when asked "why does this proof depend upon XYZ"?
In this case it's hopefully obvious enough no-one would be confused.
But you could imagine an analysis question with "you may assume the series on the right converges" and if the question asked at the end "why is this result only valid for small h" I think it would be very reasonable to not realise "because the series on the right would then diverge" was the expected answer - (particularly if it's not immediately obvious it would diverge).
Not the biggest deal in the world though.
In this case it's hopefully obvious enough no-one would be confused.
But you could imagine an analysis question with "you may assume the series on the right converges" and if the question asked at the end "why is this result only valid for small h" I think it would be very reasonable to not realise "because the series on the right would then diverge" was the expected answer - (particularly if it's not immediately obvious it would diverge).
Not the biggest deal in the world though.
For a single mark I agree it's not worth the effort to worry about it, and frankly I've not seen many (if any) questions phrased in this way. But then with today's obsession with "understanding" in exams, I sometimes get the distinct impression that the examiner's "understanding" of what they're supposed to be testing is a little lacking

Quick Reply
Related discussions
- GCSE Biology
- Differentiation
- a level maths differentiation product rule question
- Maclaurin Series Question
- Does anyone know a sheet with all the differentiated and integrated functions?
- Maths Problem
- Differentiation
- SHM
- Intergrate
- find an expression for the gradient of y=e^3.2x
- A level maths mechanics question (1)
- Help differentiation
- Help integration
- GCSE Biology
- Biology - cell differentiation
- Differentiation Question
- C3
- Implicit Differentiation 2
- Fourier series minimize integral
- maths question help
Latest
Trending
Last reply 4 days ago
Did Cambridge maths students find maths and further maths a level very easy?Last reply 2 weeks ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71
Trending
Last reply 4 days ago
Did Cambridge maths students find maths and further maths a level very easy?Last reply 2 weeks ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71



