Integrating both sides of an equation

DQd

Badges: 13

Rep:

#1

Report Thread starter 3 months ago

#1

Given the top two lines, I'm not sure how to get to/how to understand the RHS of the third line, why are limits introduced?

G,B and g are generic functions of x. The only restrictions being line 1, dB/dx>0, B(0)=0, x=[0,1]

Name: Capture.PNG
Views: 12
Size: 7.7 KB

Name: Capture.PNG
Views: 12
Size: 7.7 KB

0

reply

mqb2766

Badges: 12

Rep:

#2

Report 3 months ago

#2

(Original post by DQd)
Given the top two lines, I'm not sure how to get to/how to understand the RHS of the third line, why are limits introduced?

G,B and g are generic functions of x. The only restrictions being line 1, dB/dx>0, B(0)=0, x=[0,1]

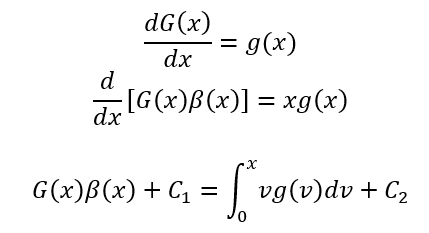
Name: Capture.PNG
Views: 12
Size: 7.7 KB

For the same reason as you have the (second) fundamental theorem of calculus
https://en.wikipedia.org/wiki/Fundam...em_of_calculus

In the 3rd equation, "x" is the point of evalulation in [0,1] on the left hand side. You integrate the right hand side from [0, x] (the limits), hence you can't have x as a dummy integration variable as well (it is "v").

Can't really see the need for the first line or both the constants in the 3rd line.

1

reply

DQd

Badges: 13

Rep:

#3

Report Thread starter 3 months ago

#3

(Original post by mqb2766)
For the same reason as you have the (second) fundamental theorem of calculus
https://en.wikipedia.org/wiki/Fundam...em_of_calculus

In the 3rd equation, "x" is the point of evalulation in [0,1] on the left hand side.

Why do we do this?

Why isn't the RHS just $\int{xg(x) dx} +C_2$

You get constants when integrating indefinitely but you can merge them.

All the other information may not be necessary, but I have a follow up question which uses this information.

0

reply

mqb2766

Badges: 12

Rep:

#4

Report 3 months ago

#4

(Original post by DQd)
Why do we do this?

Why isn't the RHS just $\int{xg(x) dx} +C_2$

You get constants when integrating indefinitely but you can merge them.

All the other information may not be necessary, but I have a follow up question which uses this information.

In the wiki link, they use "x" as the integration variable and "b" as the point at which it is evaluated. So that would mean the "b" occured on the left hand side and as the upper integraion limit and "x" as the (dummy) integration variable which goes from "a" to "b". It really doesn't matter what you call either of them, but its confusing at best to use x both as a point or value on the left hand side and i) a point (value) in the integral limit and ii) an integration variable on the right hand side.

I'd agree if it was an indefinite integral, you need one constant (not two). But post 1 is a definite integral and B(0) = 0. Again, this is equivalent to having F(a)=0 in the wiki link. So I can't see the need for either.

0

reply

DQd

Badges: 13

Rep:

#5

Report Thread starter 3 months ago

#5

(Original post by mqb2766)
In the wiki link, they use "x" as the integration variable and "b" as the point at which it is evaluated. So that would mean the "b" occured on the left hand side and as the upper integraion limit and "x" as the (dummy) integration variable which goes from "a" to "b". It really doesn't matter what you call either of them, but its confusing at best to use x both as a point or value on the left hand side and i) a point (value) in the integral limit and ii) an integration variable on the right hand side.

I'd agree if it was an indefinite integral, you need one constant (not two). But post 1 is a definite integral and B(0) = 0. Again, this is equivalent to having F(a)=0 in the wiki link. So I can't see the need for either.

The integral I'm suggesting doesn't have a limit.

The "formal statements" in the wiki article talk about limits. Why are we using limits in the first place, and how/why do we go from no limits in line 2 to limits in line 3?
Aren't we just integrating both sides w.r.t x?

You can ignore the B(0)=0 for now, we only use that fact later to get rid of the constants (not shown).

Last edited by DQd; 3 months ago

0

reply

mqb2766

Badges: 12

Rep:

#6

Report 3 months ago

#6

(Original post by DQd)
The integral I'm suggesting doesn't have a limit.

The "formal statements" in the wiki article talk about limits. Why are we using limits in the first place?
Aren't we just integrating both sides w.r.t x?

Post 1 (original question) has integration limits [0,x] where x in [0,1]? I don't know why you're using those limits as you've not explained the full problem. However it is correct as the left hand side evaluated at 0 is zero (assuming both constants are zero). This is the fundamental theorem of calculus.

Post 3 doesn't however the fact that the left hand side is evaluated at x (not stated, but assumed) and you're proposing using x as the integration variable would still not be correct.
http://mathworld.wolfram.com/DummyVariable.html

Last edited by mqb2766; 3 months ago

0

reply

DQd

Badges: 13

Rep:

#7

Report Thread starter 3 months ago

#7

(Original post by mqb2766)
Post 1 (original question) has integration limits [0,x] where x in [0,1]? I don't know why you're using those limits as you've not explained the full problem

Post 3 doesn't however the fact that the left hand side is evaluated at x (not stated, but assumed) and you're proposing using x as the integration variable would still not be correct.
http://mathworld.wolfram.com/DummyVariable.html

My question is how do we get from line 2 to line 3.
Maybe my notation was bad, it should be x \in [0,1], so I'll add more context.
x is distributed uniformly between 0 and 1, so can only take values in that interval.
I don't see why that makes it so that we must use a definite integral.

"using x as the integration variable would still not be correct."
I don't understand why this is the case, that link doesn't help.
By integrating on the RHS, isn't the point to find a function that differentiates to give xg(x)? Why do we need limits to do this/why isn't the proposed integral in post 2 ok?

Last edited by DQd; 3 months ago

0

reply

mqb2766

Badges: 12

Rep:

#8

Report 3 months ago

#8

(Original post by DQd)
Maybe my notation was bad, it should be x \in [0,1], so I'll add more context.
x is distributed uniformly between 0 and 1, so can only take values in that interval.
I don't see why that makes it so that we must use a definite integral.

"using x as the integration variable would still not be correct."
I don't understand why this is the case, that link doesn't help.
By integrating on the RHS, isn't the point to find a function that differentiates to give xg(x)? Why do we need limits to do this/why isn't the proposed integral in post 2 ok?

I'll try one last time, but will have to admit defeat if that doesn't work. I'm assuming you've gone through the wiki (or numerous other pages) and are basically happy with the fundamental theorem of calculus. In that, the limits are [a,b] and you have
F(b) - F(a) = int_a^b f(t) dt
They use the dummy integration variable "t" to break the implied similarity with "x". However, you could use f(x) dx as the integrand and that would be fine.
F(b) - F(a) = int_a^b f(x) dx
ALso
F(x) - F(a) = int_a^x f(t) dt
would be fine and you could differentiate this wrt to "x" and this would be ok.

It would not be fine to also replace both "b" and "t" with "x".
F(x) - F(a) = int_a^x f(x) dx
as on the right and side, "x" would refer to a specific value ("b") and also a dummy integration variable which ranges between "a" and "x" ("b"). You can't have a dummy integration variable which ranges betwen "a" and itself.

If you're talking about an indefinite integral, you can compute
int f(x) dx
Just be careful about what you say this is equal to (what occurs on the left hand side).

Last edited by mqb2766; 3 months ago

0

reply

DQd

Badges: 13

Rep:

#9

Report Thread starter 3 months ago

#9

(Original post by mqb2766)
I'll try one last time, but will have to admit defeat if that doesn't work. I'm assuming you've gone through the wiki (or numerous other pages) and are basically happy with the fundamental theorem of calculus. In that, the limits are [a,b] and you have
F(b) - F(a) = int_a^b f(t) dt
They use the dummy integration variable "t" to break the implied similarity with "x". However, you could use f(x) dx as the integrand and that would be fine.
F(b) - F(a) = int_a^b f(x) dx
ALso
F(x) - F(a) = int_a^x f(t) dt
would be fine and you could differentiate this wrt to x and this would be ok.

It would not be fine to also replace both b and t with x.
F(x) - F(a) = int_a^x f(x) dx
as on the right and side, x would refer to a specific value (b) and also a dummy integration variable which ranges between "0" and "x" (b). You can't have a dummy integration variable which ranges betwen 0 and itself.

If you're talking about an indefinite integral, you can compute
int f(x) dx
Just be careful about what you say this is equal to (what occurs on the left hand side).

I understand not having x in a limit when we have x in the function we are integrating.
So if I understand correctly:
Name: Capture.PNG
Views: 11
Size: 6.8 KB

Name: Capture.PNG
Views: 11
Size: 6.8 KB

(constants just to be consistent)

Then the RHS in the 3rd line is identical to my post 2? If so, I understand why I can write it like that!

Can you expand on this?
"If you're talking about an indefinite integral, you can compute int f(x) dx
Just be careful about what you say this is equal to (what occurs on the left hand side)."

0

reply

mqb2766

Badges: 12

Rep:

#10

Report 3 months ago

#10

On line 4. The second expression wouldn't really include an (indefinite integral) integration constant. You evaluate at "x" and "0" and get
F(x) - F(0)
which should be the third expression. There is no arbitrary "C" in this expression. The derivative of this
f(x)
represents how the "area" changes as you vary the upper limit "x". It does not depend on the lower limit F(0) as i) its a constant and ii) you're interested in the change in area, so this does not depend on any starting point.

The 4th line effectively says an indefinite integral is equal to a definite integral which is not correct.

0

reply

DQd

Badges: 13

Rep:

#11

Report Thread starter 3 months ago

#11

(Original post by mqb2766)
On line 4. The second expression wouldn't really include an (indefinite integral) integration constant. You evaluate at "x" and "0" and get
F(x) - F(0)
which should be the third expression. There is no arbitrary "C" in this expression. The derivative of this
f(x)
represents how the "area" changes as you vary the upper limit "x". It does not depend on the lower limit F(0) as i) its a constant and ii) you're interested in the change in area, so this does not depend on any starting point.

The 4th line effectively says an indefinite integral is equal to a definite integral which is not correct.

Ok, say the 3rd expression in line 4 is F(x)-F(0)=F(x), isn't F(x) the indefinite integral in line 2? why is that not correct?

0

reply

mqb2766

Badges: 12

Rep:

#12

Report 3 months ago

#12

(Original post by DQd)
Ok, say the 3rd expression in line 4 is F(x)-F(0)=F(x), isn't F(x) the indefinite integral in line 2? why is that not correct?

https://www.quora.com/Is-there-any-d...antiderivative
is a reasonable discussion.

The constant in the indefinite integral is -F(0) if you want to draw a parallel.

Last edited by mqb2766; 3 months ago

0

reply

DQd

Badges: 13

Rep:

#13

Report Thread starter 3 months ago

#13

Can anybody else explain this to me? All I want to know is what do we do to get from line 2 to line 3 in my original post, and why my workings above are wrong

0

reply

DFranklin

Badges: 18

Rep:

#14

Report 3 months ago

#14

(Original post by DQd)
Can anybody else explain this to me? All I want to know is what do we do to get from line 2 to line 3 in my original post,

It's just integration. If it helps, you could break it down as:

Change the variable to $\nu$ : $\dfrac{d}{d\nu} G(\nu)\beta(\nu) = \nu g(\nu)$

Integrate between 0 and x: $\displaystyle \int_0^x \dfrac{d}{d\nu} G(\nu)\beta(\nu) \,du = \int_0^x \nu g(\nu)\, d\nu$

We can integrate the LHS by FTC: $\displaystyle [G(\nu)\beta(\nu)]_0^x = \int_0^x \nu g(\nu)\, d\nu$

So we have $\displaystyle G(x)\beta(x) - G(0)\beta(0) = \int_0^x \nu g(\nu)\, d\nu$

Rewrite $-G(0) \beta(0)$ as

and we're done (ignoring the extra C_2 that serves no purpose).

1

reply

DQd

Badges: 13

Rep:

#15

Report Thread starter 2 months ago

#15

(Original post by DFranklin)
It's just integration. If it helps, you could break it down as:

Change the variable to $\nu$ : $\dfrac{d}{d\nu} G(\nu)\beta(\nu) = \nu g(\nu)$

Integrate between 0 and x: $\displaystyle \int_0^x \dfrac{d}{d\nu} G(\nu)\beta(\nu) \,du = \int_0^x \nu g(\nu)\, d\nu$

We can integrate the LHS by FTC: $\displaystyle [G(\nu)\beta(\nu)]_0^x = \int_0^x \nu g(\nu)\, d\nu$

So we have $\displaystyle G(x)\beta(x) - G(0)\beta(0) = \int_0^x \nu g(\nu)\, d\nu$

Rewrite $-G(0) \beta(0)$ as

and we're done (ignoring the extra C_2 that serves no purpose).

Thanks, the step by step helps, I understand it using limits on both sides now.

Does line 1 to 2 just come from the fact that since $\dfrac{d}{d\nu} G(\nu)\beta(\nu)$ and $\nu g(\nu)$ are given to be identical functions then the integral of each function should be identical for any of the same limits?

For a different method, does it make sense to take indefinite integrals on both sides wrt x?
Then can we consolidate the two mothods like this (I'm not certain if I'm using the constants correctly):
Name: Capture.PNG
Views: 10
Size: 16.5 KB

Name: Capture.PNG
Views: 10
Size: 16.5 KB

0

reply

DFranklin

Badges: 18

Rep:

#16

Report 2 months ago

#16

(Original post by DQd)
Thanks, the step by step helps, I understand it using limits on both sides now.

Does line 1 to 2 just come from the fact that since $\dfrac{d}{d\nu} G(\nu)\beta(\nu)$ and $\nu g(\nu)$ are given to be identical functions then the integral of each function should be identical for any of the same limits?

Yes.

For a different method, does it make sense to take indefinite integrals on both sides wrt x?
Then can we consolidate the two mothods like this (I'm not certain if I'm using the constants correctly):
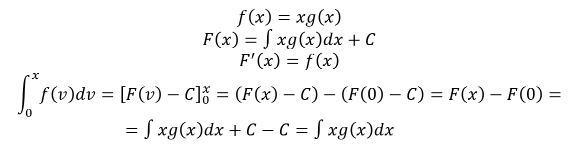
Name: Capture.PNG
Views: 10
Size: 16.5 KB

I'm not entirely sure what you are trying to say here.

Personally I would not use indefinite integrals here (and it is clear your lecturer does not want you to use indefinite integrals). To some extent this is a stylistic choice, but from experience, if you decide "I'm not going to use the stylistic choice my lecturer is using", you're gonna have a bad time.

But I really wouldn't *mix* definite and indefinite integrals, and I'm not sure what you think you're achieving by doing so. What you've done is *arguably* "correct" once you factor in the fact the the RHS integral has an arbitrary constant. But to be honest, it really isn't. Because your LHS does NOT have an arbitrary constant (i.e. we can consider it a function I(x) for a suitable choice of I), while the RHS does. So it's like writing $\log (x) = \int \dfrac{1}{x} \,dx$ . It's true for a suitable choice of the arbitrary constant, but the fact is the RHS actually evaluates to $\log(x) + C$ , so it defines an entire family of possible functions (differing by said constant).

Honestly, given you are clearly struggling with this, I would explicitly advise you to just use the definite integral approach.

0

reply

DQd

Badges: 13

Rep:

#17

Report Thread starter 2 months ago

#17

(Original post by DFranklin)
Personally I would not use indefinite integrals here (and it is clear your lecturer does not want you to use indefinite integrals).

I will use definite integrals to do this in the future, the limits are used further on in my notes anyways :P

Does it make sense for my lecturer to have constants C1 and C2 in my OP?
-If we integrate a derivative, as on the LHS in my OP, do we preserve the "true" function (with its original constsnt)?
-Why is C2 needed if we have a definite integral with limits?

(Original post by DFranklin)
But I really wouldn't *mix* definite and indefinite integrals, and I'm not sure what you think you're achieving by doing so. What you've done is *arguably* "correct" once you factor in the fact the the RHS integral has an arbitrary constant.

I'm just curious, and trying to iron out wrongs in my understanding.

Mainly, I want to know if this is ok:
Name: Capture.PNG
Views: 11
Size: 10.2 KB

^(those are brackets not absolutes, blame word!)

But to explain my last post:
Perhaps I'm abusing notation, but sometimes when you write an integral it 'implicitly' contains a constant, and sometimes you explicitly write an integral +C, and that integral "doesn't contain" a constant.

Since I define F(x) as an integral plus a contant, my final RHS integral does not really have a constant. Am I still wrong?

Last edited by DQd; 2 months ago

0

reply

DFranklin

Badges: 18

Rep:

#18

Report 2 months ago

#18

(Original post by DQd)
I will use definite integrals to do this in the future, the limits are used further on in my notes anyways :P

Does it make sense for my lecturer to have constants C1 and C2 in my OP?

Not really. But he can have two if he wants I guess...

-If we integrate a derivative, as on the LHS in my OP, do we preserve the "true" function (with its original constsnt)?

No. Differentiating loses information - you can't tell the difference between differentiating f(x) and f(x) + C.

Why is C2 needed if we have a definite integral with limits?

It isn't. But since you have an arbitary constant, adding an extra one is only superfluous, not actually problematic.

I'm just curious, and trying to iron out wrongs in my understanding.

Mainly, I want to know if this is ok:
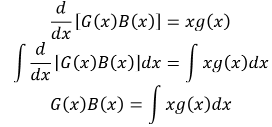
Name: Capture.PNG
Views: 11
Size: 10.2 KB

^(those are brackets not absolutes, blame word!)

But to explain my last post:
Perhaps I'm abusing notation, but sometimes when you write an integral it 'implicitly' contains a constant, and sometimes you explicitly write an integral +C, and that integral "doesn't contain" a constant.

Since I define F(x) as an integral plus a contant, my final RHS integral does not really have a constant. Am I still wrong?

Yes, I would say this is still wrong. Your RHS is an indefinite integral, so it does have a constant.

Edit: without wanting to be mean - you're insisting on trying to do this with indefinite integrals, despite everyone basically saying "don't do that". There comes a point where it's "on your own head be it". I've spent a lot of time on my replies (as has mqb) and I don't really propose to spend more on this.

Last edited by DFranklin; 2 months ago

0

reply

DQd

Badges: 13

Rep:

#19

Report Thread starter 2 months ago

#19

(Original post by DFranklin)
It isn't. But since you have an arbitary constant, adding an extra one is only superfluous, not actually problematic.

I was under the impression that C2 somehow 'came' from the RHS definite integral. That would be wrong, right?

+I'm not insisting on using indefinite integrals, and I will not use them in the future in this setting, but I wanted to understand why I can't.

Would this be correct, since both sides have (not explicitly written) constants now?
Name: Capture.PNG
Views: 9
Size: 8.1 KB

Then would this follow? If so, that's the last of it!
Name: Capture.PNG
Views: 9
Size: 3.4 KB

0

reply

DFranklin

Badges: 18

Rep:

#20

Report 2 months ago

#20

I think this is OK, but given the number of attempts, I'm forced to feel it's more by luck than judgement. I really do not think you should be using this approach.

Last edited by Lady*Stardust; 2 months ago

0

reply

Integrating both sides of an equation Watch

Quick Reply

Today on TSR

Oops, nobody has posted
in the last few hours.

See more of what you like on
The Student Room

University open days

Poll

Do you have a food intolerance or allergy?

Watched Threads

Oops, nobody has posted
in the last few hours.

See more of what you like on
The Student Room

TSR Support Team

Get Started

Using TSR

Info

TSR Group

Connect with TSR

Integrating both sides of an equation Watch

Quick Reply

Related discussions

Related university courses

Today on TSR

Oops, nobody has postedin the last few hours.

Oops, nobody is replying to posts.

See more of what you like onThe Student Room

University open days

Poll

Do you have a food intolerance or allergy?

Watched Threads

Spotlight

Oops, nobody has postedin the last few hours.

Oops, nobody is replying to posts.

See more of what you like onThe Student Room

TSR Support Team

Get Started

Using TSR

Info

TSR Group

Connect with TSR

Oops, nobody has posted
in the last few hours.

See more of what you like on
The Student Room

Oops, nobody has posted
in the last few hours.

See more of what you like on
The Student Room