What happened to the 2!? (integrating trig)
The 2 has disappeared in the integration and I am very sad because I don't know why 
I know secxtanx integrated = secx which is why it equals sec^2x but the constant 2 is just gone and I wondered if there was an explanation behind this!
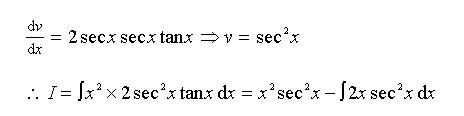
Someone explain please?

I know secxtanx integrated = secx which is why it equals sec^2x but the constant 2 is just gone and I wondered if there was an explanation behind this!
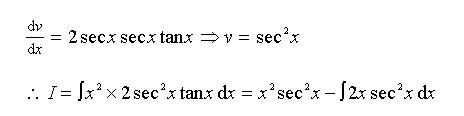
Someone explain please?

Original post by Crazydavy
Someone explain please? 

Try differentiating sec^2 x and see what you get. Use the chain rule.
Original post by Crazydavy
The 2 has disappeared in the integration and I am very sad because I don't know why 
I know secxtanx integrated = secx which is why it equals sec^2x but the constant 2 is just gone and I wondered if there was an explanation behind this!
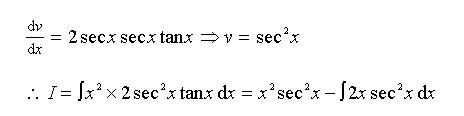
Someone explain please?

I know secxtanx integrated = secx which is why it equals sec^2x but the constant 2 is just gone and I wondered if there was an explanation behind this!
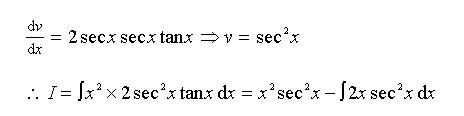
Someone explain please?

AS
your integral form is
Original post by ztibor
AS
your integral form is
your integral form is
Shouldn't it be
Because using that notation is like: (for example)

Original post by ElMoro
Shouldn't it be
Because using that notation is like: (for example)

Because using that notation is like: (for example)

means here
n can be any real (even 1) except 0 and -1
the nth derivative of f
or the second derivative
(edited 13 years ago)
Original post by ztibor
means here
n can be any real (even 1) except 0 and -1
the nth derivative of f
or the second derivative
n can be any real (even 1) except 0 and -1
the nth derivative of f
or the second derivative
It's usually a better idea to write , or if you don't want to use brackets. It's quite ambiguous notation, but when I see (where ) I interpret it to mean .
Quick Reply
Related discussions
- A level integration help
- Applied Calculus Help
- Further maths integration help
- Further maths: Further Calculus
- maths help
- Integration question
- Hardest part of A level maths
- Knowing which particular integral to use for ordinary differential equations
- A Level Maths : Common Mistakes/misconceptions
- Parametric integration
- Help urgent integration
- What have I done wrong
- what Integration technique should I be using?
- Edexcel A2 Mathematics: Core Mathematics C4 6666 01 - 22 June 2018 [Exam Discussion]
- A Level Maths Integration
- Riemann sums
- Edexcel A Level Mathematics Paper 1 (9MA0 01) - 6th June 2023 [Exam Chat]
- Maths parametric integration
- Edexcel paper 2
- Fourier Series of Sin 2x
Latest
Trending
Last reply 4 days ago
Did Cambridge maths students find maths and further maths a level very easy?Last reply 2 weeks ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71
Trending
Last reply 4 days ago
Did Cambridge maths students find maths and further maths a level very easy?Last reply 2 weeks ago
Edexcel A Level Mathematics Paper 2 unofficial mark scheme correct me if wrongMaths
71




