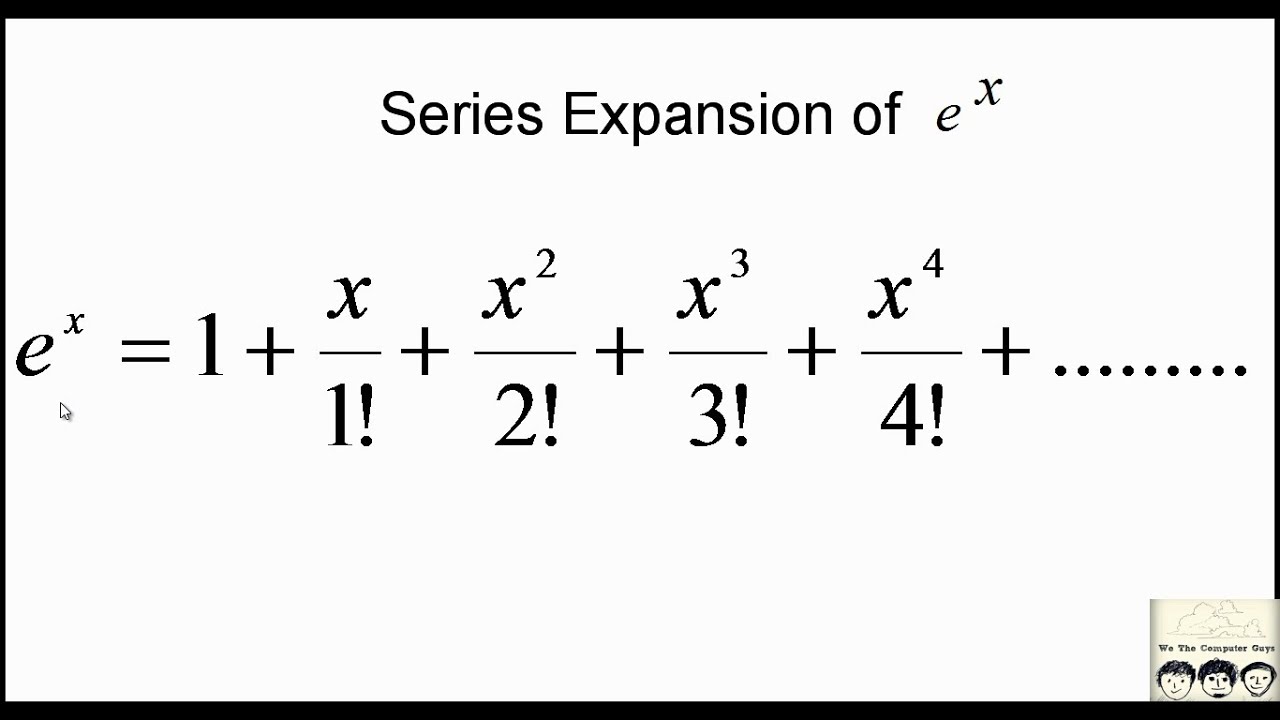Year 12s: what will be the first way you research your future options? >>

Year 12s: what will be the first way you research your future options? >>

Year 12s: what will be the first way you research your future options? >>

What's the reason for "e" not changing when being differentiated/integrated ?

I don't understand as I thought "e" was just a constant, surely any constant should just change when integrated like Pi does?

The above was phrased pretty badly.

To go further:

Why is e^x unchanged yet 3^x is when both are integrated?

(edited 6 years ago)

Scroll to see replies

It's e^x that doesn't change. e is a constant that would change when integrated or differentiated.

OP

Original post by Unown Uzer

It's e^x that doesn't change. e is a constant that would change when integrated or differentiated.

Doh

I need to go to bed lol

But then to go further, why does e^x not change when say 3^x will?

Original post by voldo

I don't understand as I thought "e" was just a constant, surely any constant should just change when integrated like Pi does?

The above was phrased pretty badly.

To go further:

Why is e^x unchanged yet 3^x is when both are integrated?

Let y = e^x

Then lny = x

And y'(1/y) = 1

And y' = y = e^x

(edited 6 years ago)

OP

Original post by Desmos

Let y = e^x

Then lny = x

And y'(1/y) = 1

And y' = y = e^x

But then I don't understand why 2.71etc^x does not change when 3^x does.

They're both positive numbers and it wont make any sense to have the decimal placed affect the reason as to why its value wont change when integrated etc.

Original post by voldo

Doh

I need to go to bed lol

But then to go further, why does e^x not change when say 3^x will?

There's no difference between the two.
(3^x)' = 3^x*ln3
(e^x)' = e^x*lne=e^x

OP

Original post by Desmos

There's no difference between the two.
(3^x)' = 3^x*ln3= 3
(e^x)' = e^x*lne=e^x

Yes, so then why can "e" not just be any number?

Since the integral of 3^x changes its value whilst e^x holds.

Since integral 3x = (3^x)/ln(3) where integral e^x is just e^x?

Original post by voldo

Yes, so then why can "e" not just be any number?

Since the integral of 3^x changes its value whilst e^x holds.

Since integral 3x = (3^x)/ln(3) where integral e^x is just e^x?

Because e is the base we're using. lne is always present. But since lne = 1, we don't include it in the derivatives/integrals. Note that d/dx(e^x)=e^xlne

OP

Original post by Desmos

Because e is the base we're using. lne is always present. But since lne = 1, we don't include it in the derivatives/integrals. Note that d/dx(e^x)=e^xlne

But then why dont we use say 7.15312521351235 instead?

I don't mean to annoy you I'm just struggling to understand why it has to specifically be this number.

Original post by voldo

But then why dont we use say 7.15312521351235 instead?

I don't mean to annoy you I'm just struggling to understand why it has to specifically be this number.

My teacher told me once that the point of e^x was to find a function st f'(x) = f(x). Now this is a very special quality which only belongs to e. The same way π is the diameter of a circle to its circumference.

Basically, e was discovered because mathematicians wanted to find f(x) so that f' = f. e^x just so happens to be that function.

Study Forum Helper

Original post by voldo

I don't understand as I thought "e" was just a constant, surely any constant should just change when integrated like Pi does?

The above was phrased pretty badly.

To go further:

Why is e^x unchanged yet 3^x is when both are integrated?

Since nobody is able to answer what you're asking...

You need to look at how

e

is defined and why there is the natural logarithm. We use the definition

\displaystyle e^x=\lim_{n\rightarrow \infty} \left( 1+\frac{x}{n} \right)^n

. Now we then have

\displaystyle \frac{d}{dx}e^x = \lim_{n\rightarrow \infty} \frac{d}{dx} \left( 1+\frac{x}{n} \right)^n

Now what is the RHS? Well by substitution we have see that it is clearly

\displaystyle \lim_{n \rightarrow \infty} \left( 1+\frac{x}{n} \right)^{n-1}

but clearly if n goes to infinity, the exponent change is completely insignificant therefore

\displaystyle \lim_{n \rightarrow \infty} \left( 1+\frac{x}{n} \right)^{n-1} = \lim_{n\rightarrow \infty} \left( 1+\frac{x}{n} \right)^n

So, we have

\displaystyle \frac{d}{dx}e^x = \lim_{n\rightarrow \infty} \left( 1+\frac{x}{n} \right)^n = e^x

thus it stays the same. and due to this beautiful flow we have the 'natural' logarithm with base e as it makes calculus much easier than any other base.

In addition to your first question, yes

e

on its own is a constant, just like

\pi

so when you integrate it you get

ex+c

and not

e^x+c

so it DOES change.

(edited 6 years ago)

if you look at the series expansion of e^x:

you can differentiate each term to get a new series... or is it new ? :holmes:

:holmes:

similarly you can integrate each term... the result should look familiar apart from a constant...

If you graph, say y = 3^x and its gradient function (y = 3^x ln3), because the gradient function is the same kind of thing just multiplied by a constant the graph of the gradient function looks very similar to the original graph.

e is just the specific number where the graph of the gradient function is exactly the same as the graph of the original function, as ln(e) = 1.

Hence if you differentiate e^x you just get e^x as the gradient function is the same as the original function.

Hope this helps :smile:

:smile:

Study Forum Helper

Original post by Steliata

If you graph, say y = 3^x and its gradient function (y = 3^x ln3), because the gradient function is the same kind of thing just multiplied by a constant the graph of the gradient function looks very similar to the original graph.

e is just the specific number where the graph of the gradient function is exactly the same as the graph of the original function, as ln(e) = 1.

Hence if you differentiate e^x you just get e^x as the gradient function is the same as the original function.

Hope this helps :smile:

:smile:

Doesn't answer the question.

Original post by RDKGames

Doesn't answer the question.

How so? I explained why e^x stays as just e^x when it's differentiated or integrated... Surely that's answering the question :/

Study Forum Helper

Original post by Steliata

How so? I explained why e^x stays as just e^x when it's differentiated or integrated... Surely that's answering the question :/

You didn't. You said that since the gradient of

e^x

is the same as the value of

e^x

at every point, you have

\frac{d}{dx}e^x =e^x

. This isn't explaining WHY it is so because the gradient is the application of the derivative. You use the derivative to FIND the gradient in the first place, doesn't work too well the other way around.

Original post by RDKGames

You didn't. You said that since the gradient of

e^x

is the same as the value of

e^x

at every point, you have

\frac{d}{dx}e^x =e^x

. This isn't explaining WHY it is so because the gradient is the application of the derivative. You use the derivative to FIND the gradient in the first place, doesn't work too well the other way around.

... I'll leave it to the mathmos then

Original post by RDKGames

Since nobody is able to answer what you're asking...

You need to look at how

e

is defined and why there is the natural logarithm. We use the definition

\displaystyle e^x=\lim_{n\rightarrow \infty} \left( 1+\frac{x}{n} \right)^n

. Now we then have

\displaystyle \frac{d}{dx}e^x = \lim_{n\rightarrow \infty} \frac{d}{dx} \left( 1+\frac{x}{n} \right)^n

This is questionable: you are swapping the order of two limiting processes (differentiation is a limiting process) without justification.

I don't want to get too thoroughly into this, because I'm not sure there's a way of doing it "well" for A-level students without papering over cracks fairly badly. But I think it should also be pointed out that there are lots of different ways of defining (which we can prove are equivalent); the definition you give is important historically, but I'm not sure it's the best way of looking at things here. [The rigourous route here I'd take is define log in terms of the integral, then define e using the inverse log function].

For what it's worth, here's an attempt at a more "intuitive" explanation of where exp(x) = lim (1+x/n)^n comes from.

Suppose we want to solve

\dfrac{dy}{dx} = y

, given y(0) = 1. So, we want to find y as a function of x. We'll assume x > 0.

Well, suppose we know y(t). Then y is increasing at the rate y(t) (since dy/dx = y), and so

y(t+h) \approx y(t) + h y(t) = (1+h) y(t)

.

And then

y(t+2h) \approx (1+h) y(t+h) = (1+h)^2 y(t)

and so on.

So if we pick h = x/N, we find

y(h) \approx (1+h), y(2h) \approx (1+h)^2

and so on, until we find

y(x) \approx(1+h)^N

, or

y(x) \approx (1+x/N)^N

.

It turns out that this gets more and more accurate as we increase N, and so we end up with the solution to

\dfrac{dy}{dx} = y

being

\displaystyle y(x) = \lim_{n\to\infty} \left(1+\dfrac{x}{n}\right)^n

A familiar process this is similar to is compound interest.

Suppose a bank pays you 100% interest every 12 months. Then after a year, £1 becomes £2.
Suppose instead the give you 50% interest every 6 months (so the same annual rate, just compounded twice as frequently). Now after a year, £1 becomes £(1.5)^2 = £2.25.
If they give (100/12)% interest every month, £1 becomes (1+1/12)^12 = £2.613.
As the compounding happens more and more frequently, the amount at the end of a year grows to

\displaystyle \lim_{n \to \infty} \left(1+\frac{1}{n}\right)^n = e

.

Original post by DFranklin

This is questionable: you are swapping the order of two limiting processes (differentiation is a limiting process) without justification.

I don't want to get too thoroughly into this, because I'm not sure there's a way of doing it "well" for A-level students without papering over cracks fairly badly. But I think it should also be pointed out that there are lots of different ways of defining (which we can prove are equivalent); the definition you give is important historically, but I'm not sure it's the best way of looking at things here. [The rigourous route here I'd take is define log in terms of the integral, then define e using the inverse log function].

Yeah, this is pretty much the only post here I agree with.

FWIW, the rigorous route I'd take (without defining

\exp

as the unique solution to

f' = f, \, \, f(0) = 1

) would be to define

\exp x

as its power series, show that it converges (absolutely) everywhere on the real line so we can interchange derivative and summation.

(for the pedants - would also show that

e^x = \exp x

)

Quick Reply

Related discussions

Latest

Trending

Trending

Articles for you

How to write an excellent personal statement in 10 steps

How to write an excellent personal statement in 10 steps

What is an LLM and how could it benefit your career?

What is an LLM and how could it benefit your career?

Powerful questions business students forget to ask their career advisers

Powerful questions business students forget to ask their career advisers

Why I chose a law degree and what studying law was like

Why I chose a law degree and what studying law was like