This discussion is now closed.
- SQE2
- MAT prep
- SQE2 prep course ULaw vs Barbri for SQE2 April 2023
- Can I do the MAT but apply during November-December?
- Physics at oxbridge
- Mat 2023
- Official MATHS applicants thread 2024
- Mat 2024
- Vet school interview help
- When to take STEP exam
- Can I do the MAT but apply during November-December?
- Can I do the MAT but apply during November-December?
- oxford maths with A*A*A
- Imperial College London Aero/EEE MAT Test
- Capgemini Invent 2024
- Warwick maths offer holder 2024
- Discrete maths '24
- Go ahead in time as far as possible
- Imperial Aero Engineering Interviews 2024
- MAT prep 2023
MAT Prep Thread - 2nd November 2016
Scroll to see replies
I didn't know that thanks!
No problem

It's in the symmetry of sin(x):

Example: Take any point on the graph here, say 70 degrees. We then see that, due to the symmetry, it is equal to 110. pi - 110 = 70; pi - 70 = 110.

It's in the symmetry of sin(x):

Example: Take any point on the graph here, say 70 degrees. We then see that, due to the symmetry, it is equal to 110. pi - 110 = 70; pi - 70 = 110.
you got any other useful trig trivia?

The syllabus says "Co-ordinate geometry and vectors in the plane". Dot product isn't in C1 or C2 so I doubt it


You probably know most or all of this but:
sin(pi/2 - x) = cos x
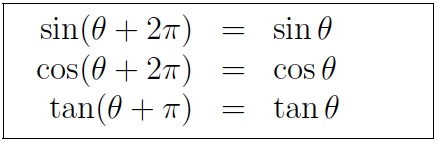

Ways to approach this?? I'm really hoping no geometry ones come up. Really would love a number theory one tho
for f set y=2^x and solve as quadratic
for i, assume log10b=0
for j, set n=1 and add up to arithmetic series together.
For 1J, you can substitute each value of n with 1 as the equation holds for n is greater or equal to 1. After doing that you find you get an arithmetic sequence 2+3+4+5...+101. Using the formula gets the answer of (d).
For 1I, you want the greatest possible value of a which means you must have the smallest possible value of b. Setting b = 1 means that it (logb)^2 = 0
So you are left with 4((loga)^2) = 1. Rearranging this leaves you with 10^1/2 which equals the square root of 10/
F: Using laws of indices we get:
2^3x + 4 = 2^2x + 2*2*(2^x)
(2^x)^3 + 4 = (2^x)^2 + 4(2^x)
let u = 2^x:
u^3 + 4 = u^2 + 4u
u^3 - u^2 - 4u + 4
factorising we get
(u - 1)(u^2 - 4)
2^x = 1 (Clearly x = 0)
u^2 = 4 => 2^x = +-2
2^x >= 0 and hence 2^x /= -2. We have two real solutions (c).
I: We want the smallest value of (log10 b)^2, which is 0, when b = 1. Therefore 4(log10 a)^2 = 1 => log10 a = 1/2 (can only take positive root). a = 10^(1/2) = sqrt(10). Answer is (c)
J: let n = 1. Therefore we have an arithmetic sequence first term 2, difference 1 and length 100.
Sum: 50(4 + 99) = 50(103) = 5150.
Therefore 5150 > k, answer (d).
For question 1D put x=1 into the equation and you end up with 1+3+5+7+...99
You can then use the sum formulae (can't remember the exact name of he equation) to get 50/2(1+99). It's fifty because it you go from x^0 to x^49 which is 50 numbers. This gives you 2500
Posted from TSR Mobile
C: Eliminate x and y respectively each time to get
(sin^2(θ) + cos^2(θ))y = y
(sin^2(θ) + cos^2(θ))x = x
Both of which are true for all values of θ as (sin^2(θ) + cos^2(θ)) = 1. Answer (a)
D: Dividing by x - 1 and getting the remainder is the same as substituting in x = 1. This gives us an arithmetic sequence length 50, difference 2, first term 1.
We sum this to get
25(2 + 98) = 25 * 100 = 2500 (b)
These are the questions I was unsure how to do question 1: D, H, I, J in the 2009 paper and I was wondering if anyone could explain how to do these questions?
Thank you so much in advance.
(iii) took quite a long time. I had to look at the solutions to do (iv) - I still don't get why the triangles and sectors subtract to get the middle par although the areas weren't too bad to calculate once I was given the sectors and triangles - but even getting 11+/15 in this question on a paper where the average successful score was 62 will really help boost your mark.
I used http://www.webmath.com/gcircle.html to draw my circles.
Hints
Spoiler
Spoiler

http://www.mathshelper.co.uk/Oxford%20Admissions%20Test%202002.pdf
These are the questions I was unsure how to do question 1: D, H, I, J in the 2009 paper and I was wondering if anyone could explain how to do these questions?
Thank you so much in advance.
D: Assume n is odd. Infront of the term involving n, which evaluates to n, we have n - 1 terms, which can be seen as pairs which always have a value of -1.
Therefore n - 1/2(n - 1) >= 100
2n - (n - 1) >= 200
n + 1 >= 200
n >= 199
The smallest value of n is 199 (c)
I: we want x^2 - 1 to be a factor. Therefore f(1) = 0 and f(-1) = 0.
f(1) = 0
n^2 - 25n + 150 = 0
(n - 10)(n - 15) = 0
n = 10, n = 15
f(-1) = 0
We need to consider when n is even or odd, as (-1)^x will be 1 if x is even and -1 if x is odd
When n is even
-n^2 + 25n - 150 = 0
-(n^2 - 25n + 150) = 0
-(n - 10)(n - 15) = 0
n = 10, n = 15
n can only be 10 here as 15 is not even
When n is odd
-n^2 - 25n - 150 = 0
-(n^2 + 25n + 150) = 0
-(n + 10)(n + 15) = 0
n = -10, n = -15
n can only be -15 here as -10 is not odd
The only consistent value of n is 10 and hence the answer is (B)
Related discussions
- SQE2
- MAT prep
- SQE2 prep course ULaw vs Barbri for SQE2 April 2023
- Can I do the MAT but apply during November-December?
- Physics at oxbridge
- Mat 2023
- Official MATHS applicants thread 2024
- Mat 2024
- Vet school interview help
- When to take STEP exam
- Can I do the MAT but apply during November-December?
- Can I do the MAT but apply during November-December?
- oxford maths with A*A*A
- Imperial College London Aero/EEE MAT Test
- Capgemini Invent 2024
- Warwick maths offer holder 2024
- Discrete maths '24
- Go ahead in time as far as possible
- Imperial Aero Engineering Interviews 2024
- MAT prep 2023
Latest
Trending
Last reply 15 hours ago
Edexcel A Level Mathematics Paper 1 (9MA0 01) - 4th June 2024 [Exam Chat]Last reply 1 week ago
Edexcel IGCSE Higher tier Mathematics A Paper 1 1H (4MA1) - 8th November 2023Last reply 1 month ago
Edexcel GCSE Mathematics Paper 3 (1MA1 3) - 13th November 2023 [Exam Chat]Last reply 1 month ago
Edexcel GCSE Statistics Paper 1 Higher Tier (1ST0 1H) - 12th June 2023 [Exam Chat]284
Last reply 1 month ago
Edexcel A Level Mathematics Paper 1 (9MA0 01) - 6th June 2023 [Exam Chat]2960
Last reply 1 month ago
AQA A Level Mathematics Paper 1 (7357/1) - 6th June 2023 [Exam Chat]352
Last reply 2 months ago
Edexcel GCSE Mathematics Paper 2 (1MA1 2) - 10th November 2023 [Exam Chat]Last reply 2 months ago
Edexcel A-level Mathematics Paper 1 [6th June 2023] Unofficial Markscheme156
Last reply 2 months ago
Edexcel GCSE Mathematics Paper 1 (1MA1 1) - 8th November 2023 [Exam Chat]Last reply 3 months ago
Edexcel IGCSE Higher tier Mathematics A Paper 1 1H (4MA1) - 19th May 2023 [Exam Chat]232
Last reply 3 months ago
AQA GCSE Mathematics Paper 3 (Higher) 8300/3H - 14th June 2023 [ Exam Chat]247
Last reply 5 months ago
Edexcel IGCSE Higher tier Mathematics A Paper 2 2H (4MA1) - 10th November 2023Last reply 8 months ago
OCR A-level Mathematics A Paper 3 (H240/03) - 20th June 2023 [Exam Chat]169
Last reply 8 months ago
AQA Level 2 Further Maths 2023 Paper 1 (8365/1) & Paper 2 (8365/2) [Exam Chat]489
Last reply 8 months ago
Edexcel A Level Mathematics Paper 3 (9MA0 03) - 20th June 2023 [Exam Chat]1836
Last reply 8 months ago
AQA A Level Mathematics Paper 3 (7357/3) - 20th June 2023 [Exam Chat]307
Last reply 8 months ago
OCR A-level Mathematics B Paper 3 (H640/03) - 20th June 2023 [Exam Chat]132
Last reply 9 months ago
Edexcel A-level Further Mathematics Paper 1 (9FM0 01) - 25th May 2023 [Exam Chat]902
Trending
Last reply 15 hours ago
Edexcel A Level Mathematics Paper 1 (9MA0 01) - 4th June 2024 [Exam Chat]Last reply 1 week ago
Edexcel IGCSE Higher tier Mathematics A Paper 1 1H (4MA1) - 8th November 2023Last reply 1 month ago
Edexcel GCSE Mathematics Paper 3 (1MA1 3) - 13th November 2023 [Exam Chat]Last reply 1 month ago
Edexcel GCSE Statistics Paper 1 Higher Tier (1ST0 1H) - 12th June 2023 [Exam Chat]284
Last reply 1 month ago
Edexcel A Level Mathematics Paper 1 (9MA0 01) - 6th June 2023 [Exam Chat]2960
Last reply 1 month ago
AQA A Level Mathematics Paper 1 (7357/1) - 6th June 2023 [Exam Chat]352
Last reply 2 months ago
Edexcel GCSE Mathematics Paper 2 (1MA1 2) - 10th November 2023 [Exam Chat]Last reply 2 months ago
Edexcel A-level Mathematics Paper 1 [6th June 2023] Unofficial Markscheme156
Last reply 2 months ago
Edexcel GCSE Mathematics Paper 1 (1MA1 1) - 8th November 2023 [Exam Chat]Last reply 3 months ago
Edexcel IGCSE Higher tier Mathematics A Paper 1 1H (4MA1) - 19th May 2023 [Exam Chat]232
Last reply 3 months ago
AQA GCSE Mathematics Paper 3 (Higher) 8300/3H - 14th June 2023 [ Exam Chat]247
Last reply 5 months ago
Edexcel IGCSE Higher tier Mathematics A Paper 2 2H (4MA1) - 10th November 2023Last reply 8 months ago
OCR A-level Mathematics A Paper 3 (H240/03) - 20th June 2023 [Exam Chat]169
Last reply 8 months ago
AQA Level 2 Further Maths 2023 Paper 1 (8365/1) & Paper 2 (8365/2) [Exam Chat]489
Last reply 8 months ago
Edexcel A Level Mathematics Paper 3 (9MA0 03) - 20th June 2023 [Exam Chat]1836
Last reply 8 months ago
AQA A Level Mathematics Paper 3 (7357/3) - 20th June 2023 [Exam Chat]307
Last reply 8 months ago
OCR A-level Mathematics B Paper 3 (H640/03) - 20th June 2023 [Exam Chat]132
Last reply 9 months ago
Edexcel A-level Further Mathematics Paper 1 (9FM0 01) - 25th May 2023 [Exam Chat]902




