Physics problem, need help.

The entrance to a harbour is a channel of length a which runs between two sandbanks a distance b apart. The banks and the channel can be assumed to be rectangular. On this particular day, there is a current of constant speed v flowing from one sandbank to the other. A yacht travelling at a constant speed relative to the water of u wants to enter the harbour.
Find the least value of u needed for the yacht to safely enter the harbour.

Someone please help me solve this and/or provide an answer, I'm struggling.

This is the classic riverboat vector problem with the usual flow of the river and boat direction transposed:



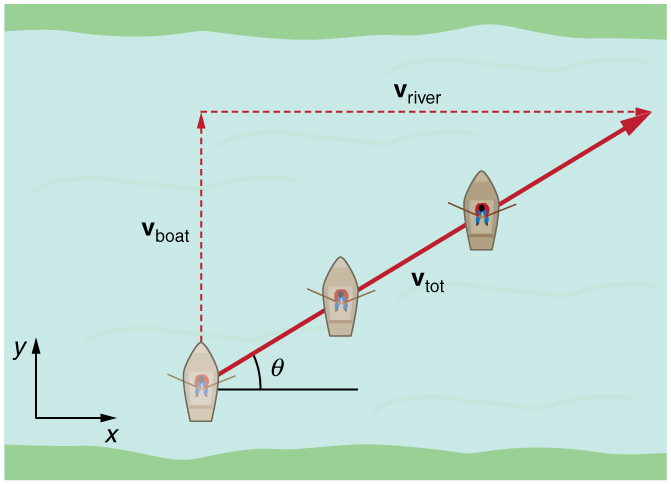
The x direction is also the length of the channel.

The y direction is the channel width and river flow direction.

The boat therefore has a y velocity component given by the river current.

So the problem is to derive an expression for the speed and direction of the boat relative to the river flow, in order to transit the length of the channel in the time it takes to cross the channel.

HINT: redraw the above diagram to comply with the labels defined by the question you posted.

Thanks, but I'm still really confused as to how I give my answer (U) in terms of V

The boat will drift at the same velocity as the current Vms^-1 between the sandbanks. The distance between the sandbanks is given as (b) metres and takes time t_drift seconds to cross from one side to the other.

$V_{drift} = \frac{b}{t_{drift}}$

rearranging for t_drift:

$t_{drift} = \frac{b}{V_{drift}}$................eq 1

For safe passage, the boat must traverse the length of the channel (a) metres before the time t_drift elapses.

$U_{boat} = \frac{a}{t_{drift}}$................eq 2

substituting eq 1

$U_{boat} = \frac{a}{(\frac{b}{V_{drift}})}$

$U_{boat} = (\frac{a}{b})V_{drift}$

removing the subscripts and complying with the minimum time requirement:

$U > \frac{aV}{b}$

Hi there, I completely understand the answer that you have given, but when I enter it apparently the boat is not necessarily travelling perpendicular to V therefore it cannot be U=av/b